11 minutes
Written: 2022-05-09 03:39 +0000
Fortran OOP and Python
This post is part of the Bridging Fortran & Python series.
Explorations of object oriented Fortran with
bind(c)derived types for representations generated by F2PY
Background
Derived types are easily one of the most visible of the modern Fortran (post-F90) features and are central to object oriented programming paradigms in Fortarn.
For those new to the language, a rough guide to some terminology:
| Fortran | Closest C/C++ equivalent |
|---|---|
| derived type | struct |
| extends type | inherited class |
| final | destructor |
| not standard conforming | undefined behaviour |
Only the first of these are actually covered in terms of
interoperability with C as of the F2018 draft
standard.
For F2PY within numpy, however, although there are no direct
equivalents in C for the more OOP specific derived types, there are
plenty of equivalent structures in Python. This post will bridge
Fortran derived types to their logically equivalent Python class
definitions.
Premise
As in the previous posts, we will be interested in a bind(c) derived type.
1type :: cartesian
2 real(c_double) :: x, y, z
3end type cartesian
Along with a simple function which uses an instance of such a derived type.
1subroutine unit_step(arg) bind(c)
2 type(cartesian), intent(inout) :: arg
3 arg%x = arg%x + 1
4 arg%y = arg%y + 1
5 arg%z = arg%z + 1
6end subroutine unit_step
To make the discussion and conversion into Python more concrete, we will start with an overview of possible representations.
Representations
The elements of the Python programming language which can be best used to emulate a derived type are (in order of relative complexity):
- Lists
- In theory, a record type can be represented and constructed from a list, with the members of the type specified in order of appearance or lexicographically. However, this is a lossy, incomplete representation as it would remove the ability to refer to and operate on the member variables by name.
- Dictionaries
- These have the benefit of being relatively simple to implement, and retain member addressable semantics.
- Named Tuples
- As immutable data structures with labels, these make good return
types, however, they are poor representations for objects which may
be modified in place (e.g. in a Fortran
subroutine). - Dataclasses
- These make sense from a logical perspective, however, they are hard to programmatically generate and use in C-extensions, limiting their utility for inter-operability with Fortran.
- Classes
- The most general and arguably the most flexible construct is to
generate code for a
PyTypeObject, which can be fleshed out to contain both attributes, as well as memory allocation rules.
Of the representations described, the first approximation covered in [a
previous post](/posts/cython-derivedtype-f2py/) was the
dictionary. A major concern 1 is that of lineage and
extensibility; python users would expect that a dictionary can be
extended with keys, which would not make much sense if the dictionary is
meant to represent a derived type. Additionally, it is difficult to
programmatically ascertain which dictionaries are meant to be
interoperable with Fortran functions or subroutines. Note that the
dictionary representation code is also present
here
with usage examples.
The rest of this post will enumerate the construction and usage of a
bind(c) derived type represented as a Python class.
Pythonic Equivalent
For a more pedagogical understanding, the derived type will be emulated (from within a Python-C exention) by the following class definition:
1class fakecart:
2 def __new__(cls, *args, **kwargs):
3 obj = object.__new__(cls)
4 obj.x = 0
5 obj.y = 0
6 obj.z = 0
7 return obj
8
9 def __init__(self, x, y, z):
10 self.x = x
11 self.y = y
12 self.z = z
13
14 def __repr__(self):
15 return f"fakecart(x: {self.x}, y: {self.y}, z: {self.z})"
16
17 def unitstep(self):
18 self.x = self.x + 1
19 self.y = self.y + 1
20 self.z = self.z +1
Note that apart from the members which mimic the those in the derived
type, for illustration’s sake we will implement the unit_step free
function as a member function.
C-Python-Fortran Implementation
For bind(c) types, we will focus on implementing the member data in
terms of C structs, and rely on bind(c) to ensure that symbols are
mangled in a compatible manner, i.e. we will not need to hardcode any
compiler specific name mangling conventions for the functions we call
from Fortran. The complete Fortran code of interest is:
1! vec.f90
2 module vec
3 use, intrinsic :: iso_c_binding
4 implicit none
5
6 type :: cartesian
7 real(c_double) :: x, y, z
8 end type cartesian
9
10 contains
11 subroutine unit_step(arg) bind(c)
12 type(cartesian), intent(inout) :: arg
13 arg%x = arg%x + 1
14 arg%y = arg%y + 1
15 arg%z = arg%z + 1
16 end subroutine unit_step
17end module vec
For a source to source translation from the Python code, we will start
with a header file containing the basic C-Fortran structures and
function declarations:
1// vecf.h
2#ifndef VECF_H_
3#define VECF_H_
4
5#include<stdio.h>
6#include<stdlib.h>
7
8// bind(c) compatible struct declaration
9typedef struct {
10 double x, y, z;
11} cartesian;
12
13// In Fortran
14void unit_step(cartesian *arg);
15
16#endif // VECF_H_
Now for the class declaration itself.
Instance Variables and Initialization
Rather than declaring double variables in the Python class, we will
opt to use the struct defined earlier.
1// CPython compatible declaration
2typedef struct {
3 PyObject_HEAD /* Do not move */
4 cartesian ccart; /* totally interoperable */
5} pycart;
This means we can initialize an object of this class by writing the
equivalent of the __init__() as:
1static int pycart_init(pycart *self, PyObject *args, PyObject *kwds) {
2 static char *kwlist[] = {"x", "y", "x", NULL};
3 if (!PyArg_ParseTupleAndKeywords(args, kwds, "|ddd", kwlist, &self->ccart.x,
4 &self->ccart.y, &self->ccart.z))
5 return -1;
6 return 0;
7}
Finally we have to declare the instance variables to be exposed from the class.
1static PyMemberDef pycart_members[] = {
2 {"x", T_DOUBLE, offsetof(pycart, ccart.x), 0, "x coordinate"},
3 {"y", T_DOUBLE, offsetof(pycart, ccart.y), 0, "y coordinate"},
4 {"z", T_DOUBLE, offsetof(pycart, ccart.z), 0, "z coordinate"},
5 {NULL} /* Sentinel */
6};
Note that in each of the snippets above, we leverage the cartesian
structure.
Class Methods
The heavy lifting of the function itself is in Fortran, while the C
struct can be used inter-operably with a derived type, leaving us with
an extremely light definition:
1static PyObject *pycart_unitstep(pycart *self) {
2 // Call Fortran on the internal representation
3 unit_step(&self->ccart);
4 Py_RETURN_NONE;
5}
We will also define a __repr()__ function for ease of interactive use:
1static PyObject *pycart_repr(pycart *self) {
2 char x[50], y[50], z[50];
3 sprintf(x, "%f", self->ccart.x);
4 sprintf(y, "%f", self->ccart.y);
5 sprintf(z, "%f", self->ccart.z);
6 PyObject *repr = PyUnicode_FromFormat("pycart(x: %s, y: %s, z: %s)", x, y, z);
7 return repr;
8}
Finally we can register the methods.
1static PyMethodDef pycart_methods[] = {
2 {"unitstep", (PyCFunction)pycart_unitstep, METH_NOARGS,
3 "Modify the class members with the Fortran unit_step function"},
4 {NULL} /* Sentinel */
5};
Before rounding out our definition:
1// Definition of type
2static PyTypeObject t_pycart = {
3 PyVarObject_HEAD_INIT(NULL, 0) /* tp_head */
4 .tp_name = "pycart.pycart",
5 .tp_doc = PyDoc_STR("One coordinate (x, y, z)"),
6 .tp_basicsize = sizeof(pycart),
7 .tp_itemsize = 0,
8 .tp_dealloc = pycart_dealloc,
9 .tp_repr = pycart_repr,
10 .tp_getattro = PyObject_GenericGetAttr,
11 .tp_setattro = PyObject_GenericSetAttr,
12 .tp_flags = Py_TPFLAGS_DEFAULT | Py_TPFLAGS_BASETYPE,
13 .tp_members = pycart_members,
14 .tp_methods = pycart_methods,
15 .tp_init = pycart_init,
16 .tp_alloc = PyType_GenericAlloc,
17 .tp_new = PyType_GenericNew,
18 .tp_free = PyObject_Del,
19};
Where we have additionally defined and bound machinery to declare
__new__().
1static void pycart_dealloc(pycart *self) {
2 // Also free the pointer here
3 Py_TYPE(self)->tp_free((PyObject *)self);
4}
5
6static PyObject *pycart_new(PyTypeObject *type, PyObject *args,
7 PyObject *kwds) {
8 // Allocate and create the cartesian object here
9 pycart *self;
10 self = (pycart *)type->tp_alloc(type, 0);
11 if (self != NULL) {
12 self->ccart.x = 0;
13 self->ccart.y = 0;
14 self->ccart.z = 0;
15 }
16 return (PyObject *)self;
17}
Boilerplate and Builds
We round off the extension by adding some doc-strings and also setting up the module itself. The code for the module itself is then:
1#ifndef PY_SSIZE_T_CLEAN
2#define PY_SSIZE_T_CLEAN
3#include <stdio.h>
4#endif /* PY_SSIZE_T_CLEAN */
5
6#include "Python.h"
7#include "structmember.h"
8
9// Fortran-C stuff
10#include "vecf.h"
11
12// Python-C stuff
13
14// CPython compatible declaration
15typedef struct {
16 PyObject_HEAD /* Do not move */
17 cartesian ccart; /* totally interoperable */
18} pycart;
19
20// Almost everything in the class must be static
21static void pycart_dealloc(pycart *self) {
22 Py_TYPE(self)->tp_free((PyObject *)self);
23}
24
25static PyObject *pycart_new(PyTypeObject *type, PyObject *args,
26 PyObject *kwds) {
27 pycart *self;
28 self = (pycart *)type->tp_alloc(type, 0);
29 if (self != NULL) {
30 self->ccart.x = 0;
31 self->ccart.y = 0;
32 self->ccart.z = 0;
33 }
34 return (PyObject *)self;
35}
36
37static int pycart_init(pycart *self, PyObject *args, PyObject *kwds) {
38 static char *kwlist[] = {"x", "y", "x", NULL};
39 if (!PyArg_ParseTupleAndKeywords(args, kwds, "|ddd", kwlist, &self->ccart.x,
40 &self->ccart.y, &self->ccart.z))
41 return -1;
42 return 0;
43}
44
45static PyMemberDef pycart_members[] = {
46 {"x", T_DOUBLE, offsetof(pycart, ccart.x), 0, "x coordinate"},
47 {"y", T_DOUBLE, offsetof(pycart, ccart.y), 0, "y coordinate"},
48 {"z", T_DOUBLE, offsetof(pycart, ccart.z), 0, "z coordinate"},
49 {NULL} /* Sentinel */
50};
51
52static PyObject *pycart_repr(pycart *self) {
53 char x[50], y[50], z[50];
54 sprintf(x, "%f", self->ccart.x);
55 sprintf(y, "%f", self->ccart.y);
56 sprintf(z, "%f", self->ccart.z);
57 PyObject *repr = PyUnicode_FromFormat("pycart(x: %s, y: %s, z: %s)", x, y, z);
58 return repr;
59}
60
61static PyObject *pycart_unitstep(pycart *self) {
62 // Call Fortran on the internal representation
63 unit_step(&self->ccart);
64 Py_RETURN_NONE;
65}
66
67static PyMethodDef pycart_methods[] = {
68 {"unitstep", (PyCFunction)pycart_unitstep, METH_NOARGS,
69 "Modify the class members with the Fortran unit_step function"},
70 {NULL} /* Sentinel */
71};
72
73// Definition of type
74static PyTypeObject t_pycart = {
75 PyVarObject_HEAD_INIT(NULL, 0) /* tp_head */
76 .tp_name = "pycart.pycart",
77 .tp_doc = PyDoc_STR("One coordinate (x, y, z)"),
78 .tp_basicsize = sizeof(pycart),
79 .tp_itemsize = 0,
80 .tp_dealloc = pycart_dealloc,
81 .tp_repr = pycart_repr,
82 .tp_getattro = PyObject_GenericGetAttr,
83 .tp_setattro = PyObject_GenericSetAttr,
84 .tp_flags = Py_TPFLAGS_DEFAULT | Py_TPFLAGS_BASETYPE,
85 .tp_members = pycart_members,
86 .tp_methods = pycart_methods,
87 .tp_init = pycart_init, /* tp_init */
88 .tp_alloc = PyType_GenericAlloc, /* tp_alloc */
89 .tp_new = PyType_GenericNew, /* tp_new */
90 .tp_free = PyObject_Del, /* tp_free */
91 // Add an attribute to show this is from Fortran
92};
93
94static char pycart_docs[] = "pycart: data type with x,y,z elements\n";
95
96static PyModuleDef pycartmodule = {PyModuleDef_HEAD_INIT, .m_name = "pycart",
97 .m_doc = pycart_docs, .m_size = -1};
98
99PyMODINIT_FUNC PyInit_pycart(void) {
100 PyObject *this_module;
101 if (PyType_Ready(&t_pycart))
102 return NULL;
103 this_module = PyModule_Create(&pycartmodule);
104 if (this_module == NULL) {
105 return NULL;
106 }
107 Py_INCREF(&t_pycart);
108 if (PyModule_AddObject(this_module, "pycart", (PyObject *)&t_pycart) < 0) {
109 Py_DECREF(&t_pycart);
110 Py_DECREF(this_module);
111 return NULL;
112 }
113 return this_module;
114}
Which is coupled with a meson.build file:
1project('pyclass_bindc', 'c', 'fortran',
2 version : '0.1',
3 default_options : ['warning_level=2',
4 'buildtype=debug',
5 'debug=true',
6 ])
7
8py_mod = import('python')
9py3 = py_mod.find_installation('python3')
10py3_dep = py3.dependency()
11message(py3.path())
12message(py3.get_install_dir())
13
14# Python Class Representation
15py3.extension_module('pycart',
16 'vec.f90',
17 'pyclassderived.c',
18 dependencies : py3_dep,
19 install : true)
Usage
This can built and used as:
1meson setup bbdir
2meson compile -C bbdir
3python -c "import bbdir.pycart as pycart; aak = pycart.pycart(1,10,2); print(aak); aak.unitstep(); print(aak)"
4pycart(x: 1.000000, y: 10.000000, z: 2.000000)
5pycart(x: 2.000000, y: 11.000000, z: 3.000000)
Conclusions
One of the best aspects of this approach is that the language pairs and
representations line up nicely to prevent any extraneous copy
operations. Representing the module subroutine as a class member
function is a design choice unlikely to be made when generating bindings
from f2py, but this was more for exploratory purposes.
To end on a rather provocative note 2, consider the timings for
the wrapped derived type pycart and its equivalent pure-Python
fakecart in Fig. 1 below:
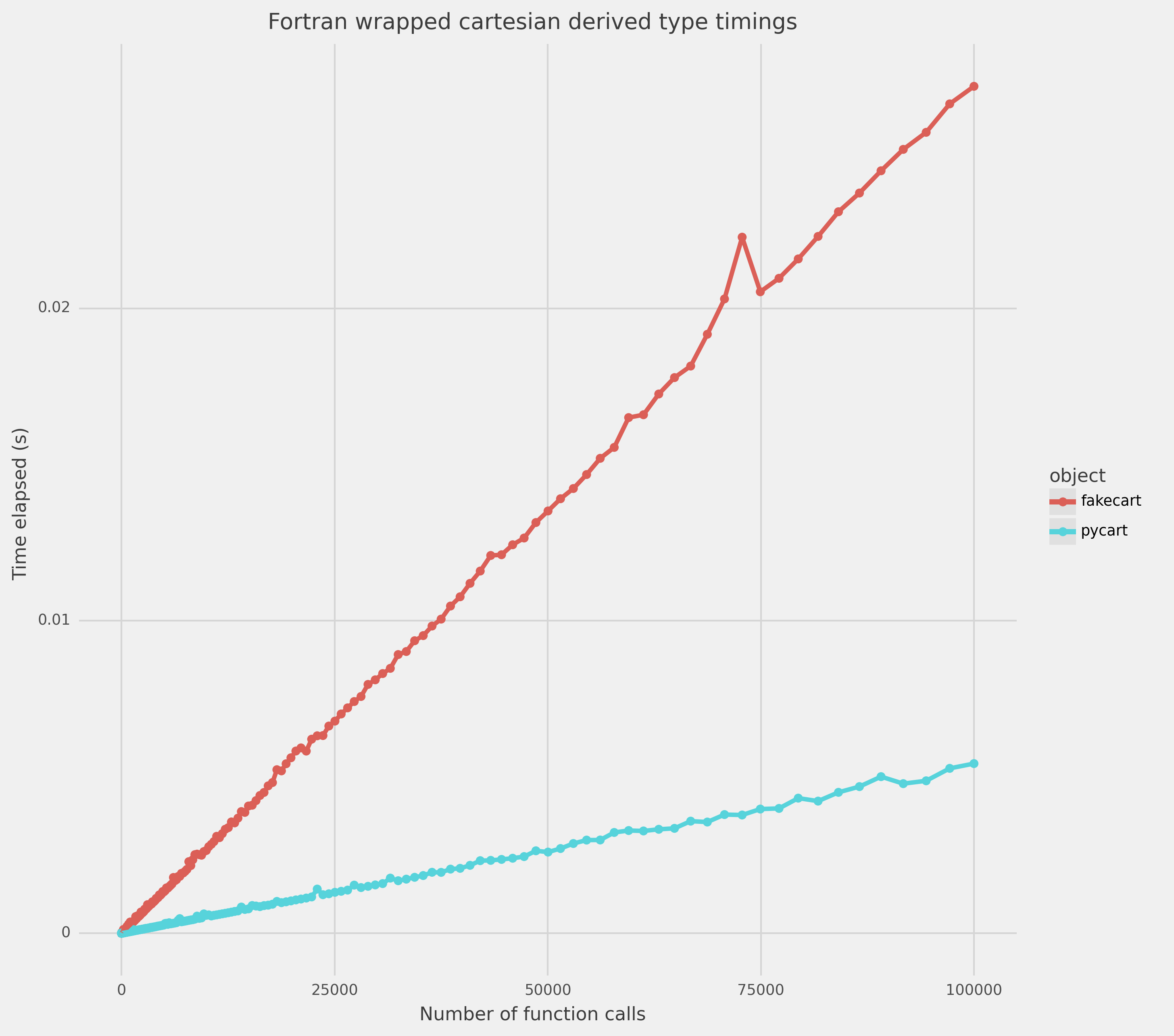
Figure 1: Results of comparing the pure-python class (fakecart) to the C-extension class backed by a Fortran derived type (pycart)
All the code for this post, along with other Fortran derived type representations is present in this repository under the examples folder.
Addendum and Future Directions
I had the pleasure of demonstrating part of this logic to fellow NumPy
maintainers Dr. Pearu Peterson and Dr. Melissa Weber Mendonça and we
were in agreement that the class strategy is the most flexible 3.
Pearu suggested leveraging pointers passed between Fortran and C in an
attempt to cover more than bind(c) compatible code, by generating
simpler Fortran wrapper functions as well, and those will likely be
among the next steps forward. The work of Pletzer et al.
(2008) is also of interest,
although their focus was on exposing a series of C functions which
call Fortran methods.
References
Pletzer, Alexander, Douglas McCune, Stefan Muszala, Srinath Vadlamani, and Scott Kruger. 2008. “Exposing Fortran Derived Types to C and Other Languages.” Computing in Science Engineering 10 (4): 86–92. https://doi.org/10.1109/MCSE.2008.94.
Noted by Adam Kelly ↩︎
Benchmarks are notoriously divisive and finicky, and no attempt was made to ensure statistical stability of the results nor were the plotted points obtained on machines dedicated and isolated from spurious loads ↩︎
I also discussed this at a few NumPy meetings and also informally mentioned this during some LFortran meetings as well ↩︎
Series info
Bridging Fortran & Python series
- NumPy, Meson and f2py
- Simple Fortran Derived Types and Python
- Exploring ISO_C_BINDING and type-bound procedures
- Fortran OOP and Python <-- You are here!
- Types from Fortran to Python via Opaque Pointers

