57 minutes
Written: 2020-02-19 07:00 +0000
ISLR :: Linear Model Selection and Regularization
Chapter VI - Linear Model Selection and Regularization
All the questions are as per the ISL seventh printing of the First edition1.
Common
Instead of using the standard functions, we will leverage the mlr3
package2.
1#install.packages("mlr3","data.table","mlr3viz","mlr3learners")
Actually for R version 3.6.2, the steps to get it working were a bit
more involved.
Load ISLR and other libraries.
1libsUsed<-c("dplyr","ggplot2","tidyverse",
2 "ISLR","caret","MASS", "gridExtra",
3 "pls","latex2exp","data.table")
4invisible(lapply(libsUsed, library, character.only = TRUE))
Question 6.8 - Page 262
In this exercise, we will generate simulated data, and will then use this data to perform best subset selection.
(a) Use the =rnorm()=function to generate a predictor \(X\) of length \(n = 100\), as well as a noise vector \(\eta\) of length \(n = 100\).
(b) Generate a response vector \(Y\) of length \(n = 100\) according to the model \[Y = \beta_0 + \beta_1X + \beta2X^2 + \beta_3X^3 + \eta\], where \(\beta_{0}\) , \(\beta_{1}\), \(\beta_{2}\), and \(\beta_{3}\) are constants of your choice.
(c) Use the regsubsets() function to perform best subset selection
in order to choose the best model containing the predictors \(X\),
\(X^{2}\), …, \(X^{10}\). What is the best model obtained according to
\(C_p\) , BIC, and adjusted \(R^2\) ? Show some plots to provide evidence
for your answer, and report the coefficients of the best model obtained.
Note you will need to use the data.frame() function to create a single
data set containing both \(X\) and \(Y\).
(d) Repeat (c), using forward stepwise selection and also using backwards stepwise selection. How does your answer compare to the results in (c)?
(e) Now fit a lasso model to the simulated data, again using \(X\), \(X^{2}\), …, \(X^{10}\) as predictors. Use cross-validation to select the optimal value of \(\lambda\). Create plots of the cross-validation error as a function of \(\lambda\). Report the resulting coefficient estimates, and discuss the results obtained.
(f) Now generate a response vector Y according to the model \[Y = \beta_{0} + \beta_{7}X^{7} + \eta,\] and perform best subset selection and the lasso. Discuss the results obtained.
Answer
a) Generate model
1set.seed(1984)
2x<-rnorm(100)
3noise<-rnorm(100)
b) Response vector
1beta=c(43,5,3,6)
2y<-beta[1] + beta[2]*x + beta[3]*x^2 + beta[4]*x^3 + noise
3qplot(x,y)
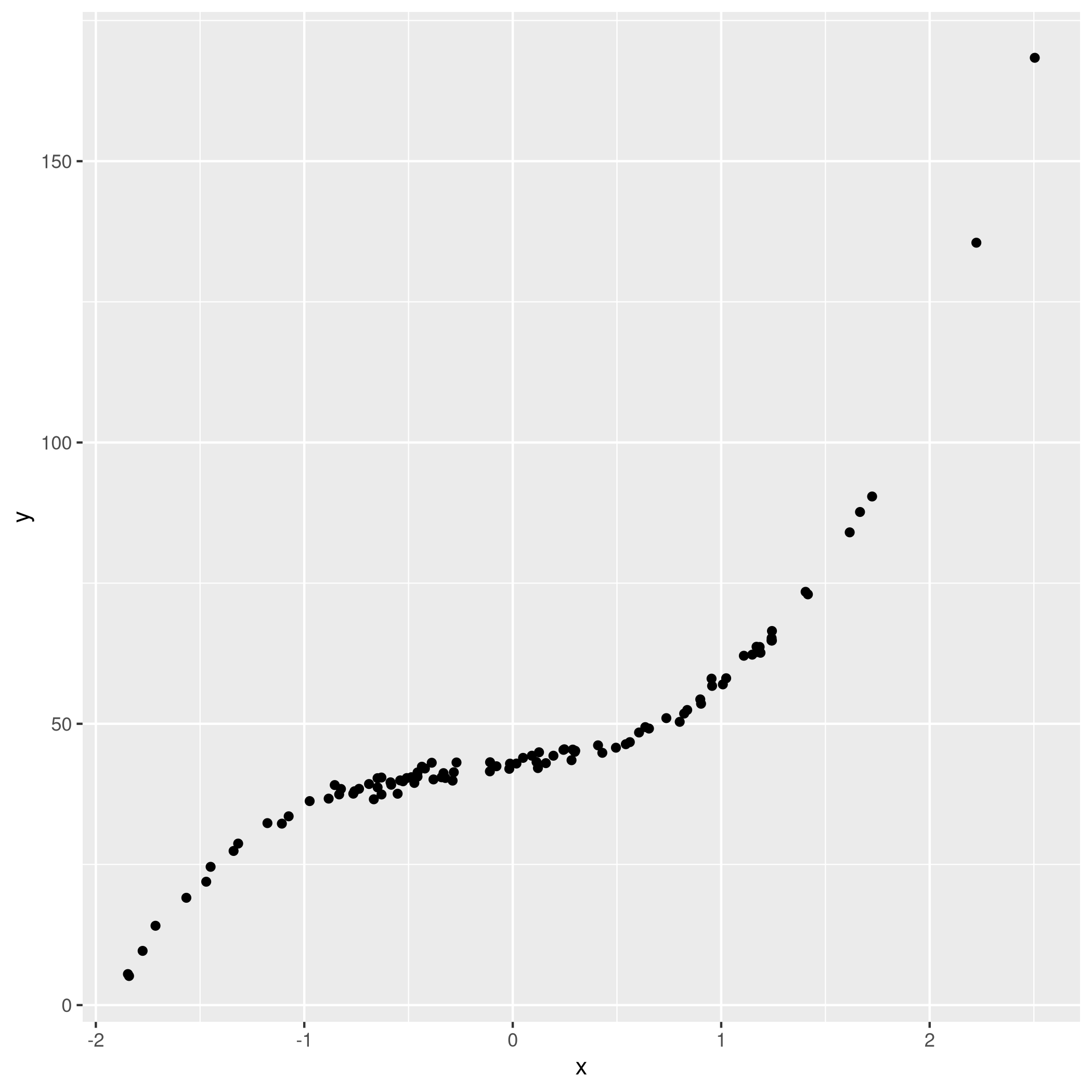
c) Subset selection
Since the question requires it, we will be using the leaps libraries.
1library(leaps)
2df<-data.frame(y=y,x=x)
3sets=regsubsets(y~poly(x,10,raw=T),data=df,nvmax=10)
4sets %>% summary
1## Subset selection object
2## Call: regsubsets.formula(y ~ poly(x, 10, raw = T), data = df, nvmax = 10)
3## 10 Variables (and intercept)
4## Forced in Forced out
5## poly(x, 10, raw = T)1 FALSE FALSE
6## poly(x, 10, raw = T)2 FALSE FALSE
7## poly(x, 10, raw = T)3 FALSE FALSE
8## poly(x, 10, raw = T)4 FALSE FALSE
9## poly(x, 10, raw = T)5 FALSE FALSE
10## poly(x, 10, raw = T)6 FALSE FALSE
11## poly(x, 10, raw = T)7 FALSE FALSE
12## poly(x, 10, raw = T)8 FALSE FALSE
13## poly(x, 10, raw = T)9 FALSE FALSE
14## poly(x, 10, raw = T)10 FALSE FALSE
15## 1 subsets of each size up to 10
16## Selection Algorithm: exhaustive
17## poly(x, 10, raw = T)1 poly(x, 10, raw = T)2 poly(x, 10, raw = T)3
18## 1 ( 1 ) " " " " "*"
19## 2 ( 1 ) " " "*" "*"
20## 3 ( 1 ) "*" "*" "*"
21## 4 ( 1 ) "*" "*" "*"
22## 5 ( 1 ) "*" "*" "*"
23## 6 ( 1 ) "*" " " "*"
24## 7 ( 1 ) "*" "*" "*"
25## 8 ( 1 ) "*" "*" "*"
26## 9 ( 1 ) "*" "*" "*"
27## 10 ( 1 ) "*" "*" "*"
28## poly(x, 10, raw = T)4 poly(x, 10, raw = T)5 poly(x, 10, raw = T)6
29## 1 ( 1 ) " " " " " "
30## 2 ( 1 ) " " " " " "
31## 3 ( 1 ) " " " " " "
32## 4 ( 1 ) "*" " " " "
33## 5 ( 1 ) " " " " " "
34## 6 ( 1 ) "*" " " "*"
35## 7 ( 1 ) "*" " " "*"
36## 8 ( 1 ) "*" "*" "*"
37## 9 ( 1 ) "*" " " "*"
38## 10 ( 1 ) "*" "*" "*"
39## poly(x, 10, raw = T)7 poly(x, 10, raw = T)8 poly(x, 10, raw = T)9
40## 1 ( 1 ) " " " " " "
41## 2 ( 1 ) " " " " " "
42## 3 ( 1 ) " " " " " "
43## 4 ( 1 ) " " " " " "
44## 5 ( 1 ) " " " " "*"
45## 6 ( 1 ) " " "*" " "
46## 7 ( 1 ) " " "*" " "
47## 8 ( 1 ) " " "*" " "
48## 9 ( 1 ) "*" "*" "*"
49## 10 ( 1 ) "*" "*" "*"
50## poly(x, 10, raw = T)10
51## 1 ( 1 ) " "
52## 2 ( 1 ) " "
53## 3 ( 1 ) " "
54## 4 ( 1 ) " "
55## 5 ( 1 ) "*"
56## 6 ( 1 ) "*"
57## 7 ( 1 ) "*"
58## 8 ( 1 ) "*"
59## 9 ( 1 ) "*"
60## 10 ( 1 ) "*"
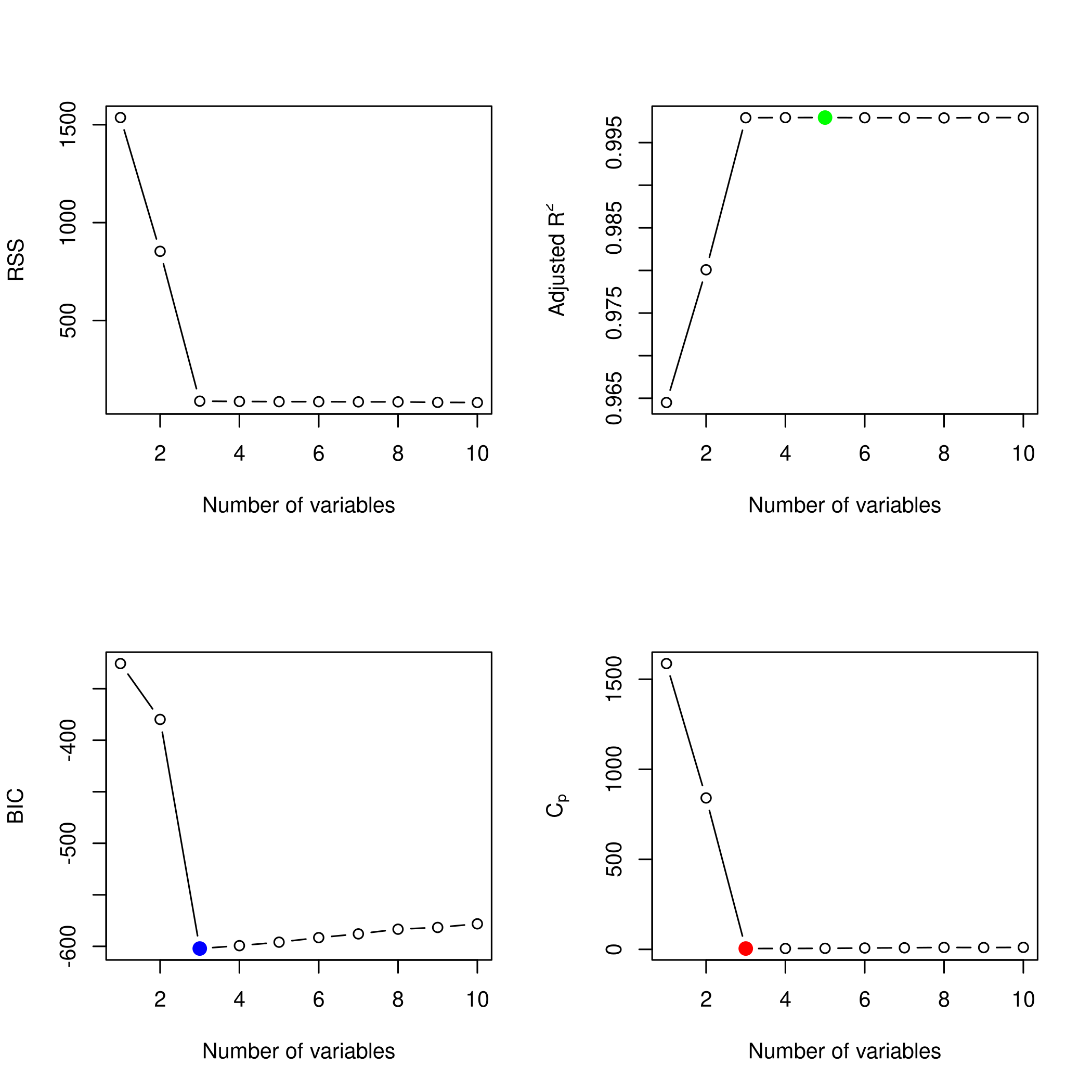
We also want the best parameters.
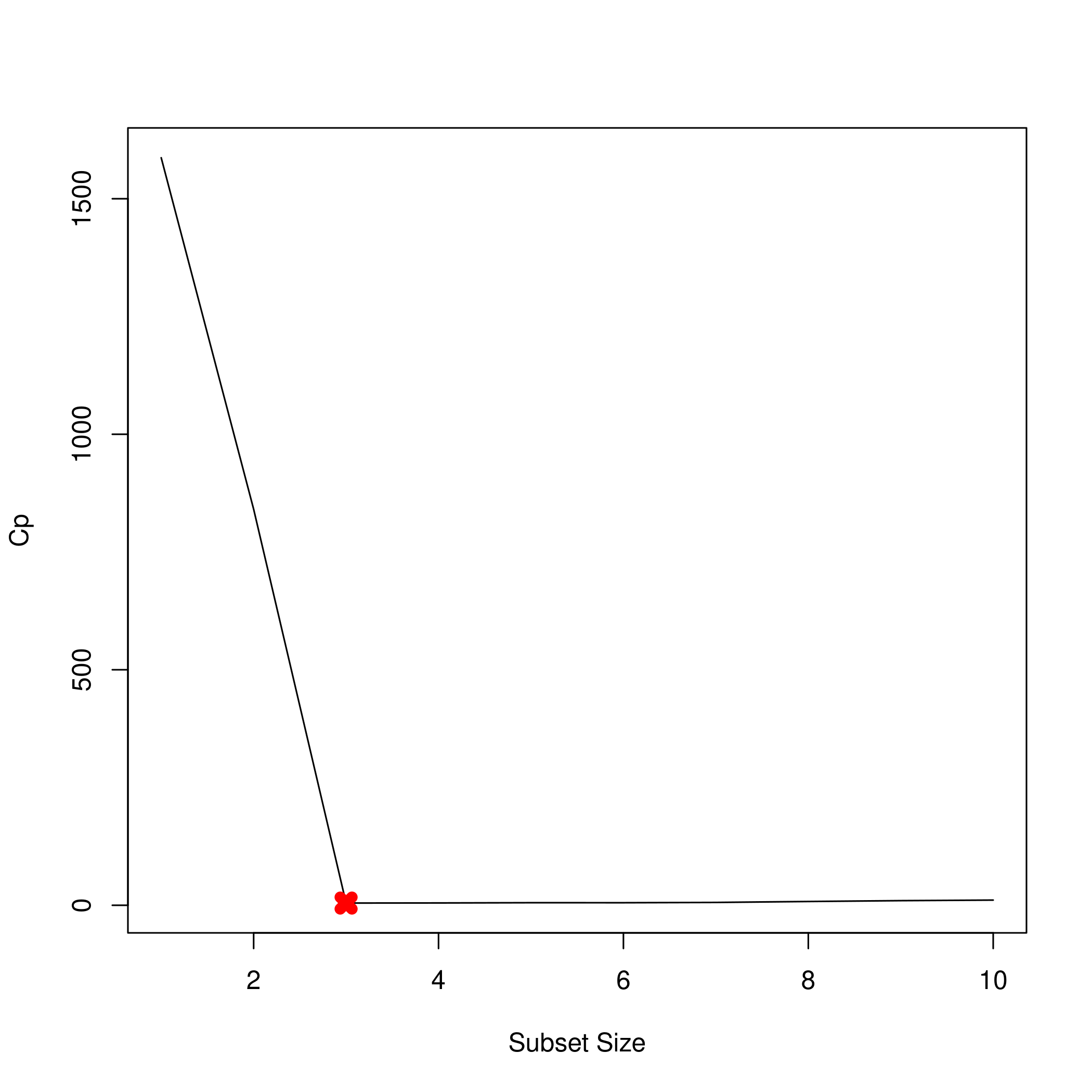
1summarySet<-summary(sets)
2which.min(summarySet$cp) %>% print
1## [1] 3
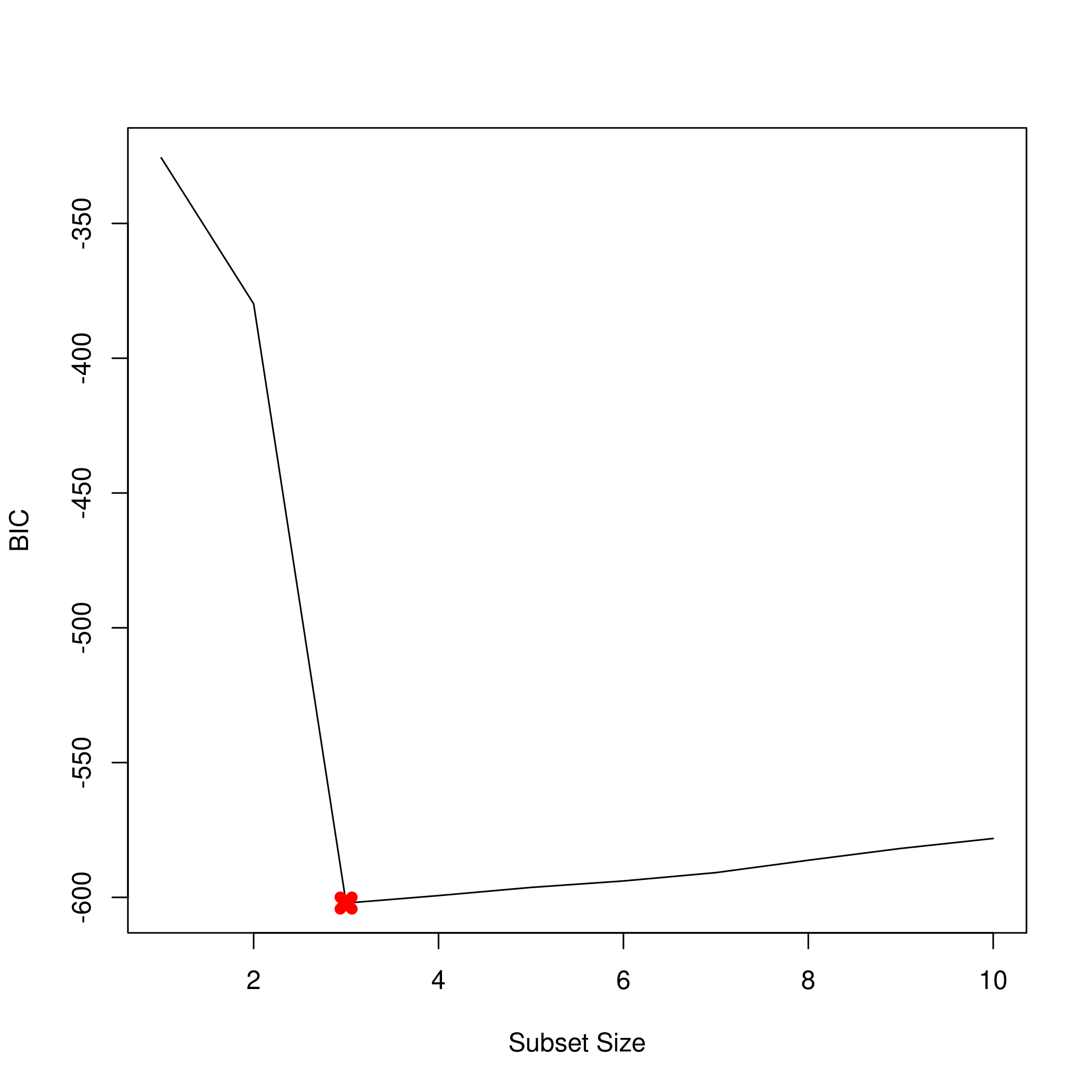
1which.min(summarySet$bic) %>% print
1## [1] 3
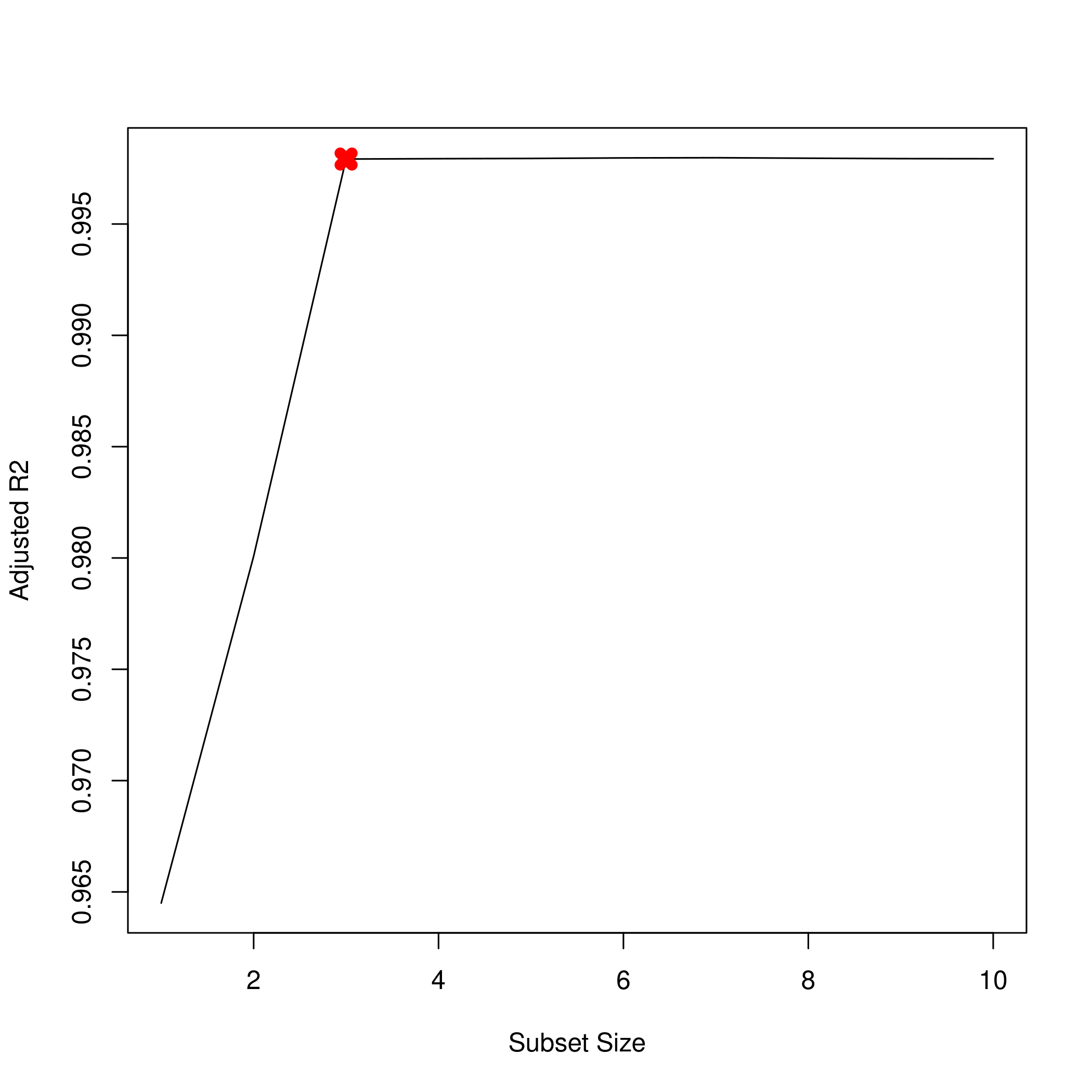
1which.max(summarySet$adjr2) %>% print
1## [1] 7
We might want to see this as a plot.
1plot(summarySet$cp, xlab = "Subset Size", ylab = "Cp", pch = 20, type = "l")
2points(3,summarySet$cp[3],pch=4,col='red',lwd=7)
1plot(summarySet$bic, xlab = "Subset Size", ylab = "BIC", pch = 20, type = "l")
2points(3,summarySet$bic[3],pch=4,col='red',lwd=7)
1plot(summarySet$adjr2, xlab = "Subset Size", ylab = "Adjusted R2", pch = 20, type = "l")
2points(3,summarySet$adjr2[3],pch=4,col='red',lwd=7)
Lets check the coefficients.
1coefficients(sets,id=3) %>% print
1## (Intercept) poly(x, 10, raw = T)1 poly(x, 10, raw = T)2
2## 42.895657 5.108094 3.034408
3## poly(x, 10, raw = T)3
4## 5.989367
1beta %>% print
1## [1] 43 5 3 6
We see that we actually have a pretty good set of coefficients.
d) Forward and backward stepwise models
1modelX<-poly(x,10,raw=T)
2forwardFit<-regsubsets(y~modelX,data=df,nvmax=10,method="forward")
3forwardFit %>% summary %>% print
1## Subset selection object
2## Call: regsubsets.formula(y ~ modelX, data = df, nvmax = 10, method = "forward")
3## 10 Variables (and intercept)
4## Forced in Forced out
5## modelX1 FALSE FALSE
6## modelX2 FALSE FALSE
7## modelX3 FALSE FALSE
8## modelX4 FALSE FALSE
9## modelX5 FALSE FALSE
10## modelX6 FALSE FALSE
11## modelX7 FALSE FALSE
12## modelX8 FALSE FALSE
13## modelX9 FALSE FALSE
14## modelX10 FALSE FALSE
15## 1 subsets of each size up to 10
16## Selection Algorithm: forward
17## modelX1 modelX2 modelX3 modelX4 modelX5 modelX6 modelX7 modelX8
18## 1 ( 1 ) " " " " "*" " " " " " " " " " "
19## 2 ( 1 ) " " "*" "*" " " " " " " " " " "
20## 3 ( 1 ) "*" "*" "*" " " " " " " " " " "
21## 4 ( 1 ) "*" "*" "*" "*" " " " " " " " "
22## 5 ( 1 ) "*" "*" "*" "*" "*" " " " " " "
23## 6 ( 1 ) "*" "*" "*" "*" "*" " " " " " "
24## 7 ( 1 ) "*" "*" "*" "*" "*" " " "*" " "
25## 8 ( 1 ) "*" "*" "*" "*" "*" " " "*" "*"
26## 9 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"
27## 10 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"
28## modelX9 modelX10
29## 1 ( 1 ) " " " "
30## 2 ( 1 ) " " " "
31## 3 ( 1 ) " " " "
32## 4 ( 1 ) " " " "
33## 5 ( 1 ) " " " "
34## 6 ( 1 ) " " "*"
35## 7 ( 1 ) " " "*"
36## 8 ( 1 ) " " "*"
37## 9 ( 1 ) " " "*"
38## 10 ( 1 ) "*" "*"
We might want to take a look at these.
1par(mfrow=c(2,2))
2plot(forwardFit)
3plot(forwardFit,scale='Cp')
4plot(forwardFit,scale='r2')
5plot(forwardFit,scale='adjr2')
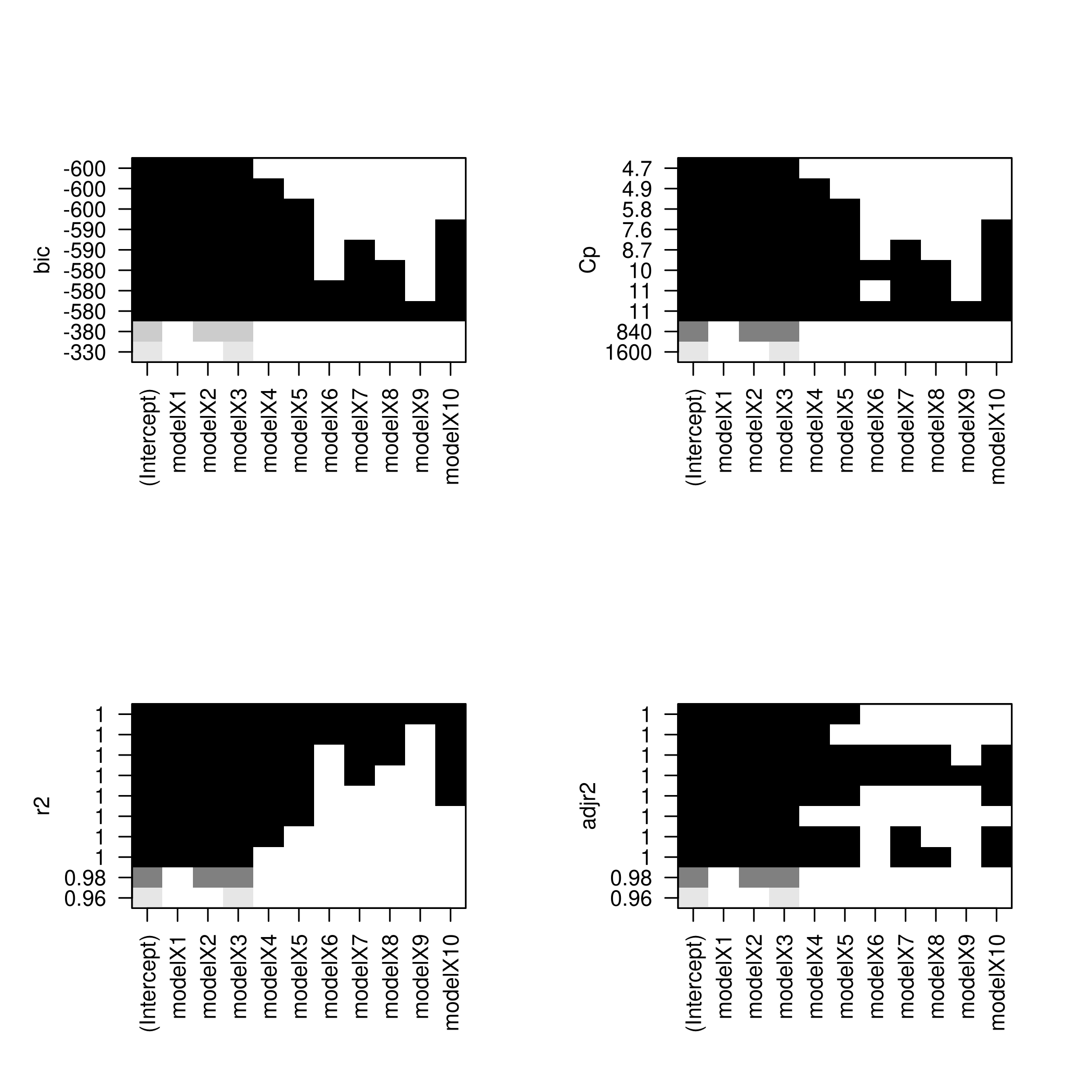
I find these not as fun to look at, so we will do better.
1plotLEAP=function(leapObj){
2 par(mfrow = c(2,2))
3 bar2=which.max(leapObj$adjr2)
4 bbic=which.min(leapObj$bic)
5 bcp=which.min(leapObj$cp)
6 plot(leapObj$rss,xlab="Number of variables",ylab="RSS",type="b")
7 plot(leapObj$adjr2,xlab="Number of variables",ylab=TeX("Adjusted R^2"),type="b")
8 points(bar2,leapObj$adjr2[bar2],col="green",cex=2,pch=20)
9 plot(leapObj$bic,xlab="Number of variables",ylab=TeX("BIC"),type="b")
10 points(bbic,leapObj$bic[bbic],col="blue",cex=2,pch=20)
11 plot(leapObj$cp,xlab="Number of variables",ylab=TeX("C_p"),type="b")
12 points(bcp,leapObj$cp[bcp],col="red",cex=2,pch=20)
13}
1plotLEAP(forwardFit %>% summary)
Lets check the backward selection as well.
1modelX<-poly(x,10,raw=T)
2backwardFit<-regsubsets(y~modelX,data=df,nvmax=10,method="backward")
3backwardFit %>% summary %>% print
1## Subset selection object
2## Call: regsubsets.formula(y ~ modelX, data = df, nvmax = 10, method = "backward")
3## 10 Variables (and intercept)
4## Forced in Forced out
5## modelX1 FALSE FALSE
6## modelX2 FALSE FALSE
7## modelX3 FALSE FALSE
8## modelX4 FALSE FALSE
9## modelX5 FALSE FALSE
10## modelX6 FALSE FALSE
11## modelX7 FALSE FALSE
12## modelX8 FALSE FALSE
13## modelX9 FALSE FALSE
14## modelX10 FALSE FALSE
15## 1 subsets of each size up to 10
16## Selection Algorithm: backward
17## modelX1 modelX2 modelX3 modelX4 modelX5 modelX6 modelX7 modelX8
18## 1 ( 1 ) " " " " "*" " " " " " " " " " "
19## 2 ( 1 ) "*" " " "*" " " " " " " " " " "
20## 3 ( 1 ) "*" " " "*" "*" " " " " " " " "
21## 4 ( 1 ) "*" " " "*" "*" " " "*" " " " "
22## 5 ( 1 ) "*" " " "*" "*" " " "*" " " "*"
23## 6 ( 1 ) "*" " " "*" "*" " " "*" " " "*"
24## 7 ( 1 ) "*" "*" "*" "*" " " "*" " " "*"
25## 8 ( 1 ) "*" "*" "*" "*" " " "*" "*" "*"
26## 9 ( 1 ) "*" "*" "*" "*" " " "*" "*" "*"
27## 10 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"
28## modelX9 modelX10
29## 1 ( 1 ) " " " "
30## 2 ( 1 ) " " " "
31## 3 ( 1 ) " " " "
32## 4 ( 1 ) " " " "
33## 5 ( 1 ) " " " "
34## 6 ( 1 ) " " "*"
35## 7 ( 1 ) " " "*"
36## 8 ( 1 ) " " "*"
37## 9 ( 1 ) "*" "*"
38## 10 ( 1 ) "*" "*"
We might want to take a look at these.
1par(mfrow=c(2,2))
2plot(backwardFit)
3plot(backwardFit,scale='Cp')
4plot(backwardFit,scale='r2')
5plot(backwardFit,scale='adjr2')
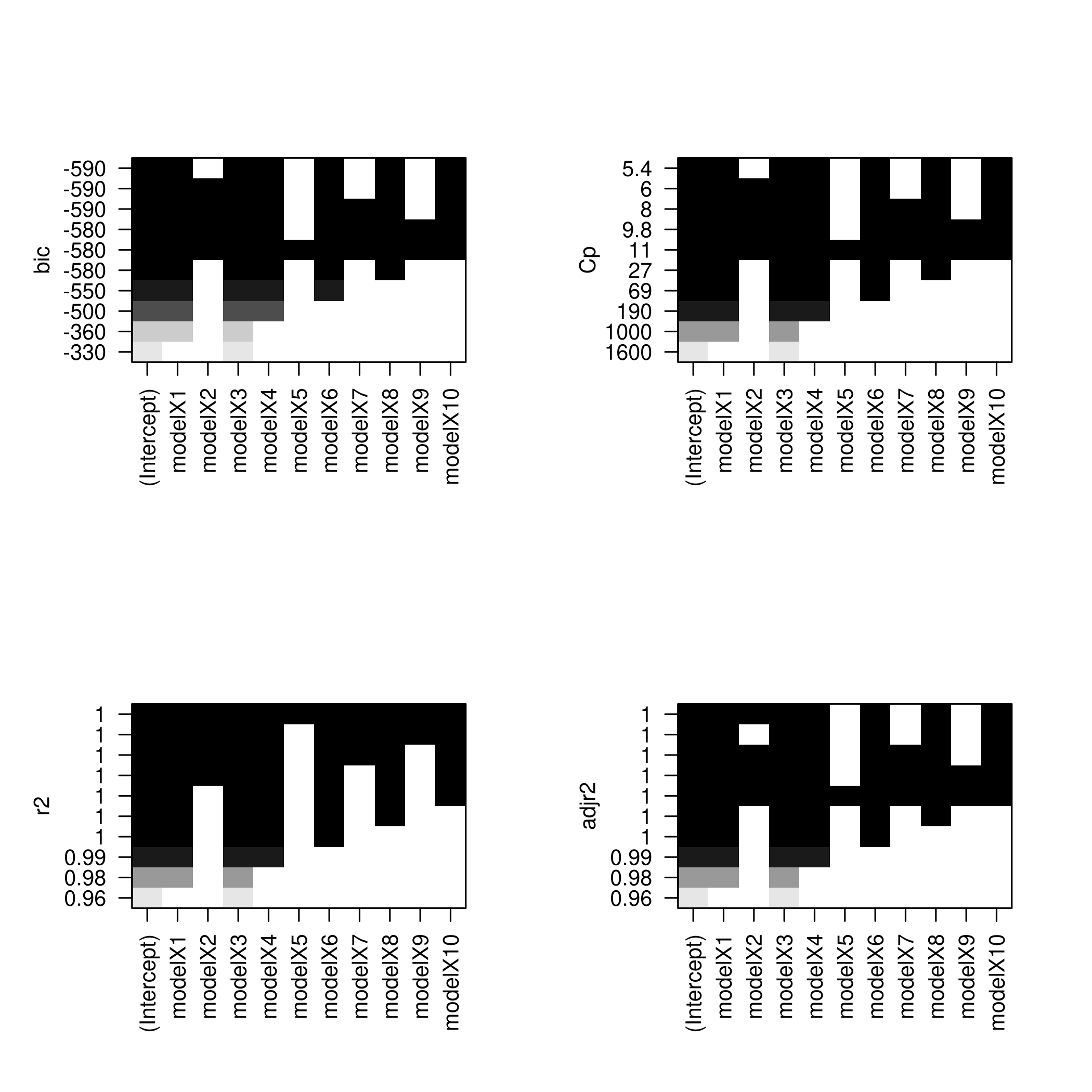
1plotLEAP(backwardFit %>% summary)
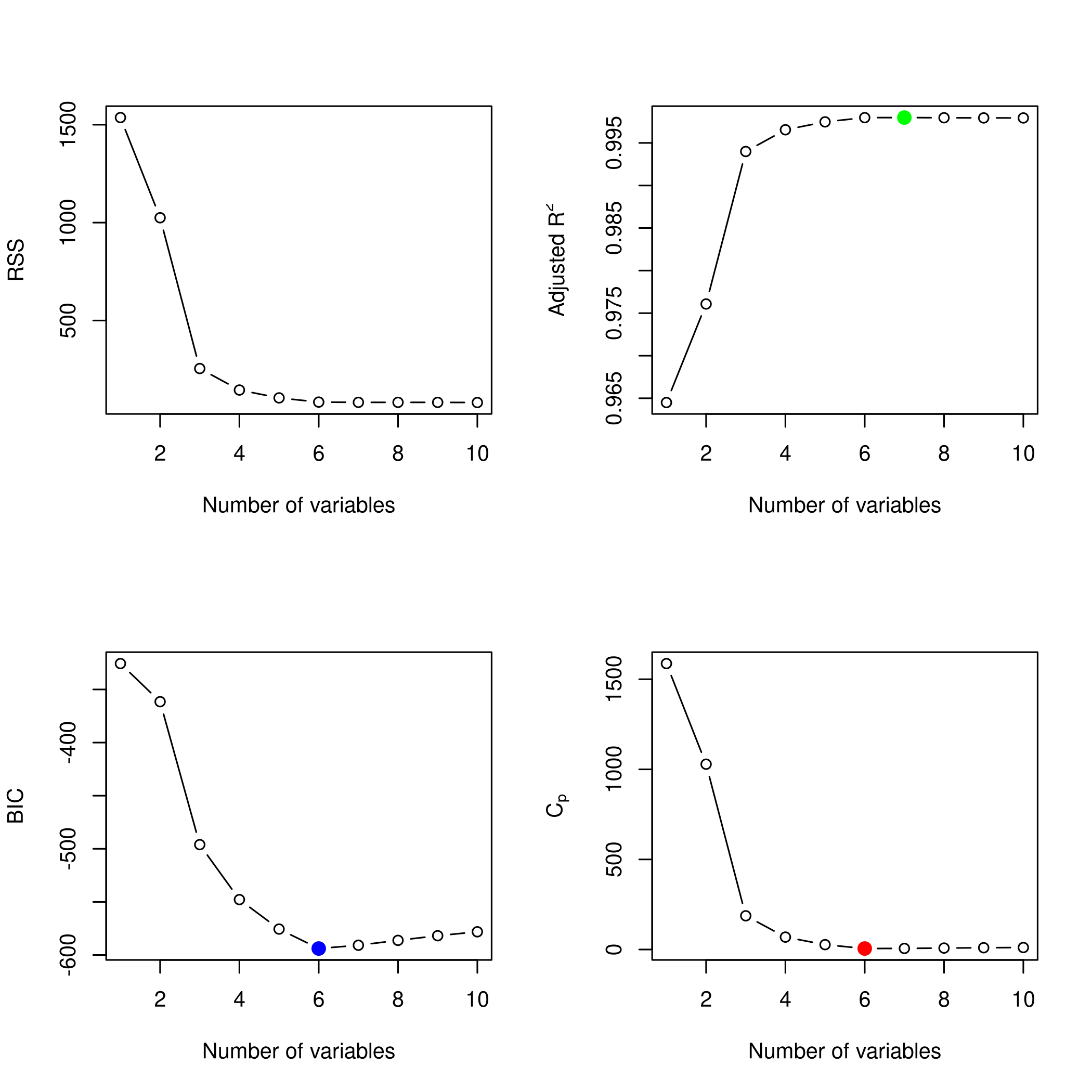
In spite of some slight variations, overall all methods converge to the
same best set of parameters, that of the third model.
e) LASSO and Cross Validation
For this, instead of using glmnet directly, we will use caret.
1df<-df %>% mutate(x2=x^2,x3=x^3,
2 x4=x^4,x5=x^5,
3 x6=x^6,x7=x^7,
4 x8=x^8,x9=x^9,
5 x10=x^10)
1lambda<-10^seq(-3, 3, length = 100)
2lassoCaret= train(y~.,data=df,method="glmnet",tuneGrid=expand.grid(alpha=1,lambda=lambda))
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1lassoCaret %>% print
1## glmnet
2##
3## 100 samples
4## 10 predictor
5##
6## No pre-processing
7## Resampling: Bootstrapped (25 reps)
8## Summary of sample sizes: 100, 100, 100, 100, 100, 100, ...
9## Resampling results across tuning parameters:
10##
11## lambda RMSE Rsquared MAE
12## 1.000000e-03 1.009696 0.9965632 0.8051425
13## 1.149757e-03 1.009696 0.9965632 0.8051425
14## 1.321941e-03 1.009696 0.9965632 0.8051425
15## 1.519911e-03 1.009696 0.9965632 0.8051425
16## 1.747528e-03 1.009696 0.9965632 0.8051425
17## 2.009233e-03 1.009696 0.9965632 0.8051425
18## 2.310130e-03 1.009696 0.9965632 0.8051425
19## 2.656088e-03 1.009696 0.9965632 0.8051425
20## 3.053856e-03 1.009696 0.9965632 0.8051425
21## 3.511192e-03 1.009696 0.9965632 0.8051425
22## 4.037017e-03 1.009696 0.9965632 0.8051425
23## 4.641589e-03 1.009696 0.9965632 0.8051425
24## 5.336699e-03 1.009696 0.9965632 0.8051425
25## 6.135907e-03 1.009696 0.9965632 0.8051425
26## 7.054802e-03 1.009696 0.9965632 0.8051425
27## 8.111308e-03 1.009696 0.9965632 0.8051425
28## 9.326033e-03 1.009696 0.9965632 0.8051425
29## 1.072267e-02 1.009696 0.9965632 0.8051425
30## 1.232847e-02 1.009696 0.9965632 0.8051425
31## 1.417474e-02 1.009696 0.9965632 0.8051425
32## 1.629751e-02 1.009696 0.9965632 0.8051425
33## 1.873817e-02 1.009696 0.9965632 0.8051425
34## 2.154435e-02 1.009696 0.9965632 0.8051425
35## 2.477076e-02 1.009696 0.9965632 0.8051425
36## 2.848036e-02 1.009696 0.9965632 0.8051425
37## 3.274549e-02 1.009696 0.9965632 0.8051425
38## 3.764936e-02 1.009696 0.9965632 0.8051425
39## 4.328761e-02 1.009696 0.9965632 0.8051425
40## 4.977024e-02 1.009696 0.9965632 0.8051425
41## 5.722368e-02 1.009696 0.9965632 0.8051425
42## 6.579332e-02 1.009696 0.9965632 0.8051425
43## 7.564633e-02 1.009637 0.9965632 0.8050666
44## 8.697490e-02 1.009216 0.9965637 0.8047862
45## 1.000000e-01 1.008901 0.9965636 0.8046468
46## 1.149757e-01 1.009470 0.9965616 0.8054790
47## 1.321941e-01 1.011206 0.9965561 0.8074253
48## 1.519911e-01 1.014475 0.9965476 0.8104930
49## 1.747528e-01 1.019202 0.9965383 0.8147296
50## 2.009233e-01 1.025943 0.9965259 0.8203974
51## 2.310130e-01 1.035374 0.9965094 0.8284187
52## 2.656088e-01 1.048294 0.9964878 0.8393282
53## 3.053856e-01 1.065717 0.9964592 0.8530952
54## 3.511192e-01 1.088903 0.9964215 0.8701072
55## 4.037017e-01 1.119433 0.9963715 0.8918217
56## 4.641589e-01 1.158919 0.9963053 0.9193677
57## 5.336699e-01 1.209841 0.9962136 0.9532842
58## 6.135907e-01 1.275467 0.9960778 0.9957151
59## 7.054802e-01 1.357247 0.9958966 1.0471169
60## 8.111308e-01 1.457886 0.9956561 1.1087362
61## 9.326033e-01 1.580743 0.9953362 1.1818188
62## 1.072267e+00 1.729330 0.9949070 1.2696235
63## 1.232847e+00 1.907599 0.9943306 1.3758463
64## 1.417474e+00 2.120178 0.9935518 1.5059031
65## 1.629751e+00 2.369642 0.9924954 1.6673393
66## 1.873817e+00 2.662906 0.9910539 1.8621728
67## 2.154435e+00 3.007271 0.9890638 2.0978907
68## 2.477076e+00 3.409377 0.9863097 2.3788439
69## 2.848036e+00 3.864727 0.9825900 2.7053428
70## 3.274549e+00 4.350785 0.9778541 3.0659309
71## 3.764936e+00 4.847045 0.9724311 3.4403210
72## 4.328761e+00 5.369017 0.9668240 3.8351441
73## 4.977024e+00 5.919492 0.9626812 4.2512694
74## 5.722368e+00 6.562134 0.9580843 4.7389049
75## 6.579332e+00 7.307112 0.9534537 5.2945905
76## 7.564633e+00 8.132296 0.9500300 5.8774541
77## 8.697490e+00 9.067321 0.9486589 6.4760997
78## 1.000000e+01 10.167822 0.9483195 7.1226569
79## 1.149757e+01 11.473284 0.9482975 7.8556639
80## 1.321941e+01 13.002703 0.9482975 8.6990451
81## 1.519911e+01 14.727852 0.9454119 9.6414650
82## 1.747528e+01 16.325210 0.9426796 10.5303097
83## 2.009233e+01 17.740599 0.9357286 11.3560865
84## 2.310130e+01 18.585795 0.9227167 11.8799668
85## 2.656088e+01 18.939596 0.9080584 12.1336575
86## 3.053856e+01 19.123568 0.9109065 12.2733471
87## 3.511192e+01 19.197966 NaN 12.3308613
88## 4.037017e+01 19.197966 NaN 12.3308613
89## 4.641589e+01 19.197966 NaN 12.3308613
90## 5.336699e+01 19.197966 NaN 12.3308613
91## 6.135907e+01 19.197966 NaN 12.3308613
92## 7.054802e+01 19.197966 NaN 12.3308613
93## 8.111308e+01 19.197966 NaN 12.3308613
94## 9.326033e+01 19.197966 NaN 12.3308613
95## 1.072267e+02 19.197966 NaN 12.3308613
96## 1.232847e+02 19.197966 NaN 12.3308613
97## 1.417474e+02 19.197966 NaN 12.3308613
98## 1.629751e+02 19.197966 NaN 12.3308613
99## 1.873817e+02 19.197966 NaN 12.3308613
100## 2.154435e+02 19.197966 NaN 12.3308613
101## 2.477076e+02 19.197966 NaN 12.3308613
102## 2.848036e+02 19.197966 NaN 12.3308613
103## 3.274549e+02 19.197966 NaN 12.3308613
104## 3.764936e+02 19.197966 NaN 12.3308613
105## 4.328761e+02 19.197966 NaN 12.3308613
106## 4.977024e+02 19.197966 NaN 12.3308613
107## 5.722368e+02 19.197966 NaN 12.3308613
108## 6.579332e+02 19.197966 NaN 12.3308613
109## 7.564633e+02 19.197966 NaN 12.3308613
110## 8.697490e+02 19.197966 NaN 12.3308613
111## 1.000000e+03 19.197966 NaN 12.3308613
112##
113## Tuning parameter 'alpha' was held constant at a value of 1
114## RMSE was used to select the optimal model using the smallest value.
115## The final values used for the model were alpha = 1 and lambda = 0.1.
1lassoCaret %>% ggplot
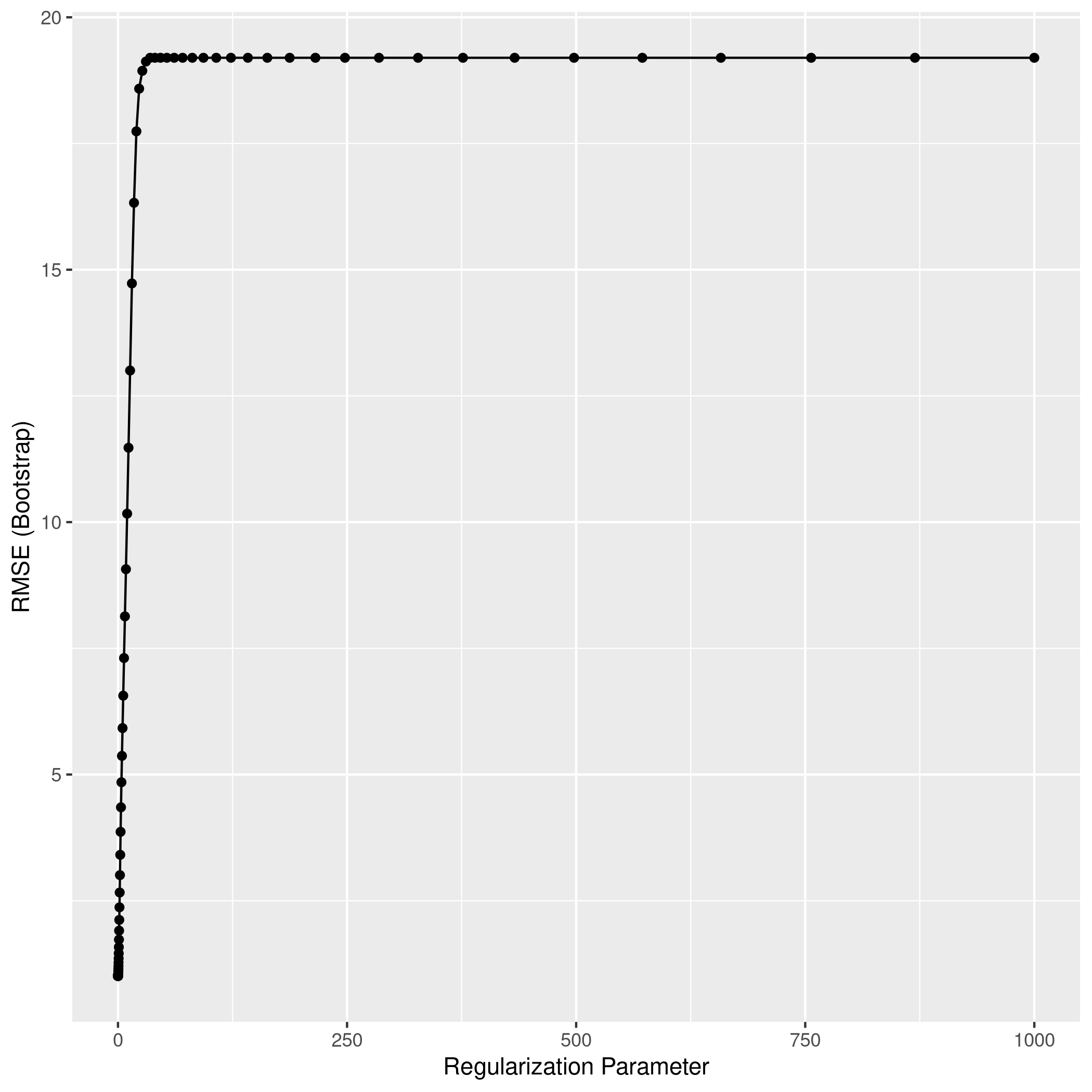
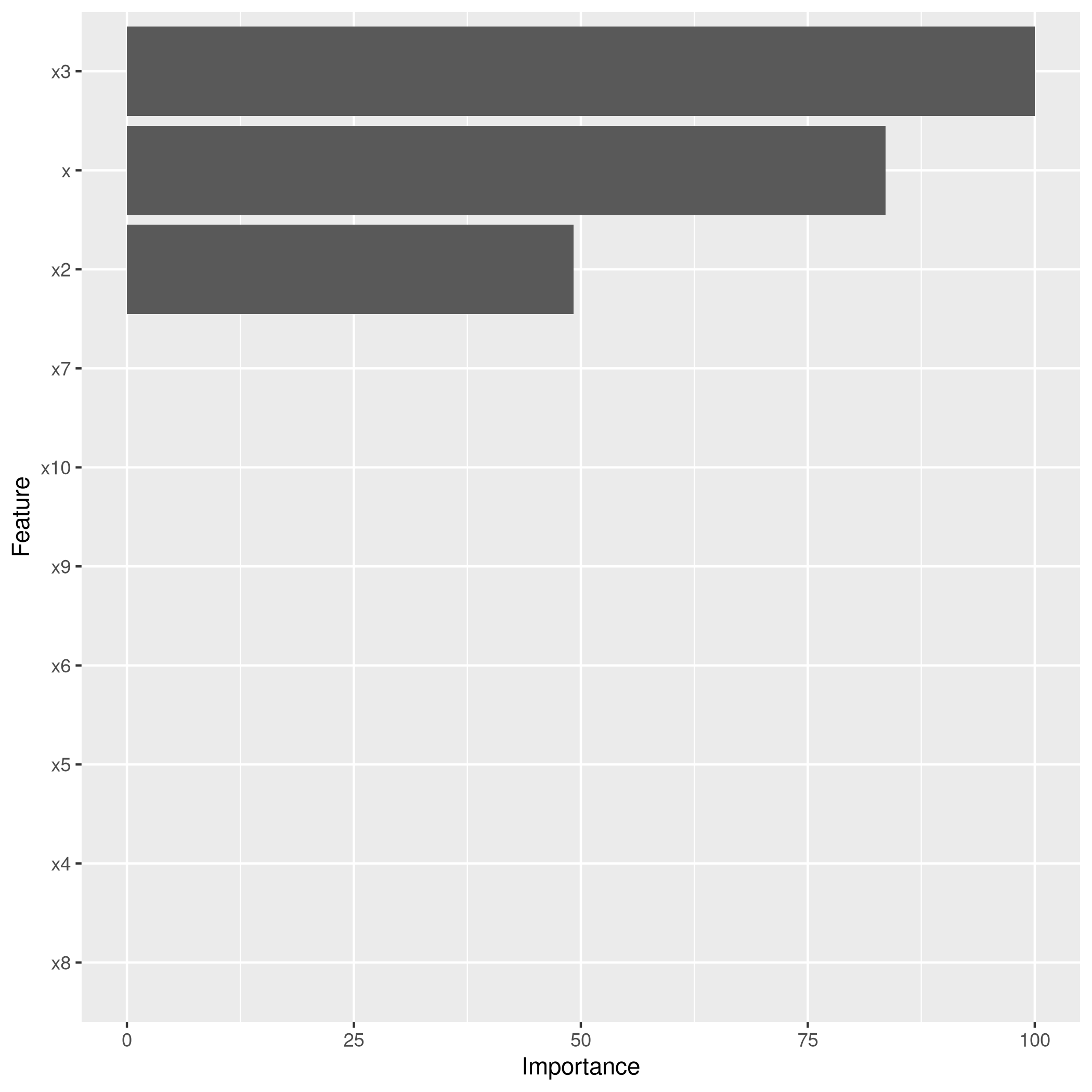
1lassoCaret %>% varImp %>% ggplot
1library(glmnet)
1## Loading required package: Matrix
1##
2## Attaching package: 'Matrix'
1## The following objects are masked from 'package:tidyr':
2##
3## expand, pack, unpack
1## Loaded glmnet 3.0-2
1library(boot)
1##
2## Attaching package: 'boot'
1## The following object is masked from 'package:lattice':
2##
3## melanoma
1lasso.mod <- cv.glmnet(as.matrix(df[-1]), y, alpha=1)
2lambda <- lasso.mod$lambda.min
3plot(lasso.mod)
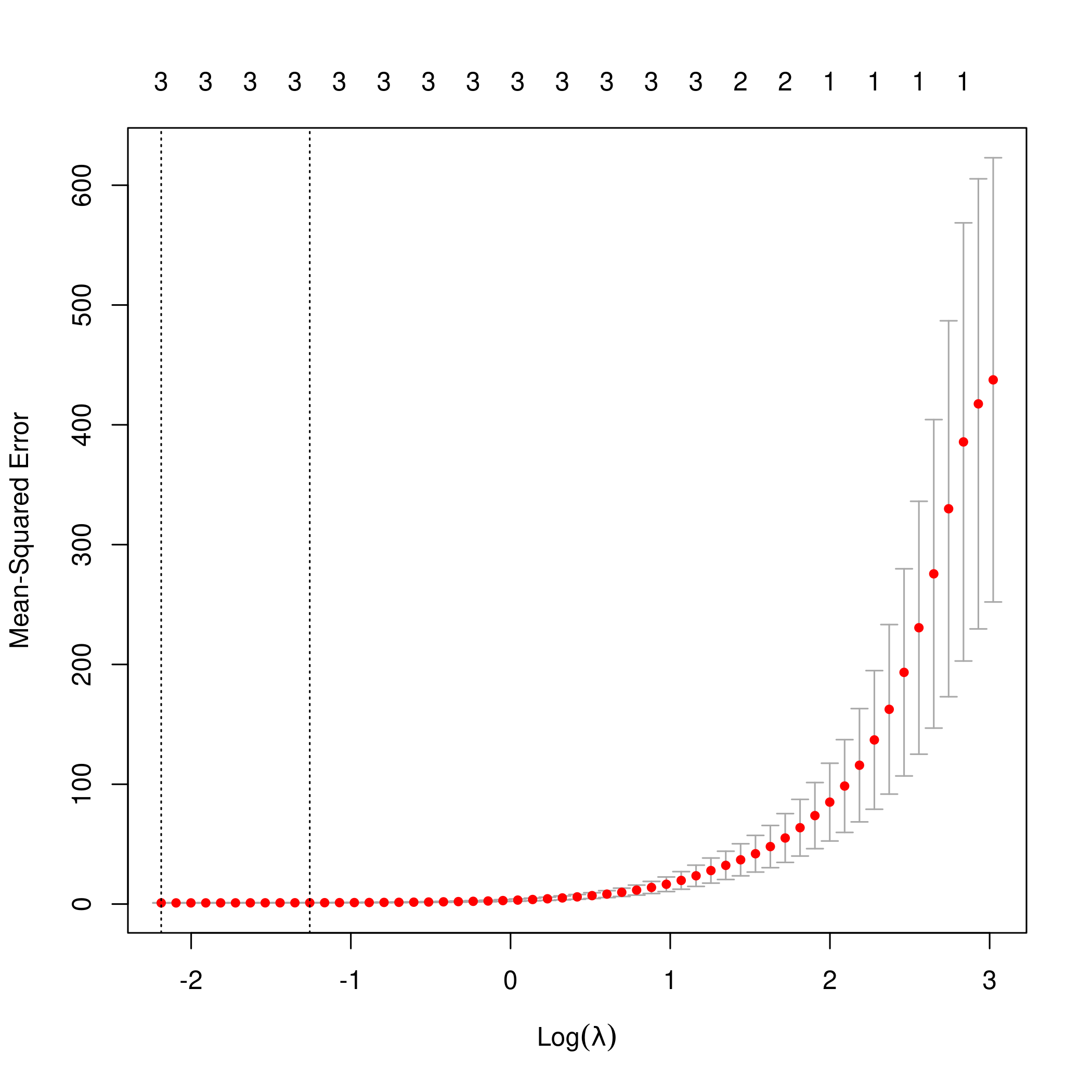
1predict(lasso.mod, s=lambda, type="coefficients")
1## 11 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) 42.975240
4## x 5.005023
5## x2 2.947540
6## x3 5.989105
7## x4 .
8## x5 .
9## x6 .
10## x7 .
11## x8 .
12## x9 .
13## x10 .
Clearly, the only important variables are \(x\), \(x^2\) and \(x^3\).
f) New model
Our new model requires a newly expanded set of betas as well.
1y2<-beta[1]+23*x^7+noise
1modelX<-poly(x,10,raw=T)
2newDF<-data.frame(x=as.matrix(modelX),y=y2)
3newSub<-regsubsets(y2~.,data=newDF,nvmax=10)
4newSub %>% summary
1## Subset selection object
2## Call: regsubsets.formula(y2 ~ ., data = newDF, nvmax = 10)
3## 11 Variables (and intercept)
4## Forced in Forced out
5## x.1 FALSE FALSE
6## x.2 FALSE FALSE
7## x.3 FALSE FALSE
8## x.4 FALSE FALSE
9## x.5 FALSE FALSE
10## x.6 FALSE FALSE
11## x.7 FALSE FALSE
12## x.8 FALSE FALSE
13## x.9 FALSE FALSE
14## x.10 FALSE FALSE
15## y FALSE FALSE
16## 1 subsets of each size up to 10
17## Selection Algorithm: exhaustive
18## x.1 x.2 x.3 x.4 x.5 x.6 x.7 x.8 x.9 x.10 y
19## 1 ( 1 ) " " " " " " " " " " " " " " " " " " " " "*"
20## 2 ( 1 ) " " " " " " " " "*" " " " " " " " " " " "*"
21## 3 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " "*"
22## 4 ( 1 ) "*" "*" "*" " " " " " " " " " " " " " " "*"
23## 5 ( 1 ) "*" "*" "*" " " " " " " " " " " " " "*" "*"
24## 6 ( 1 ) "*" "*" "*" "*" "*" " " " " " " " " " " "*"
25## 7 ( 1 ) "*" "*" "*" "*" "*" " " "*" " " " " " " "*"
26## 8 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " " " " " " "*"
27## 9 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " " "*" " " "*"
28## 10 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" " " "*" "*"
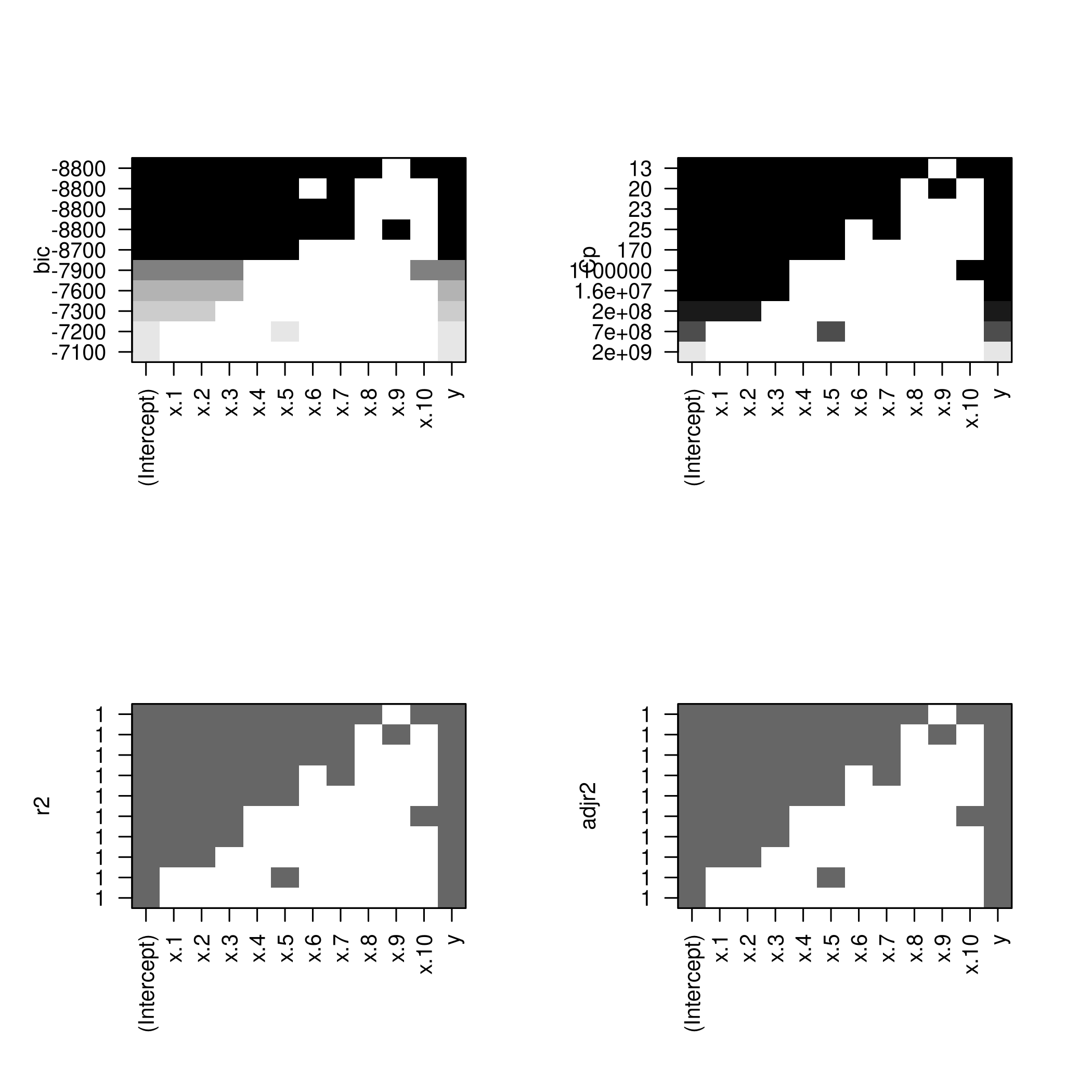
1plotLEAP(newSub %>% summary)
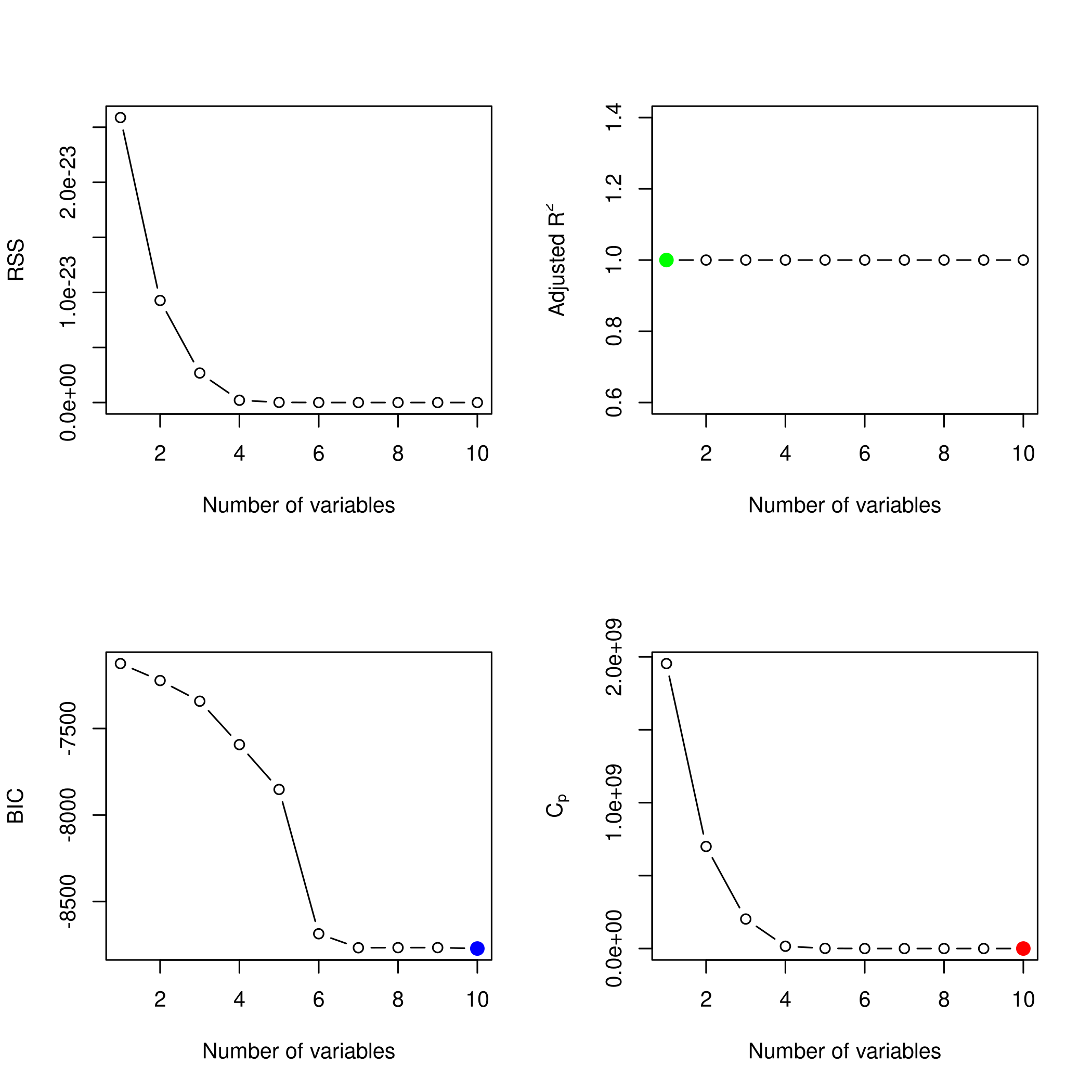
Or in its more native look,
1par(mfrow=c(2,2))
2plot(newSub)
3plot(newSub,scale='Cp')
4plot(newSub,scale='r2')
5plot(newSub,scale='adjr2')
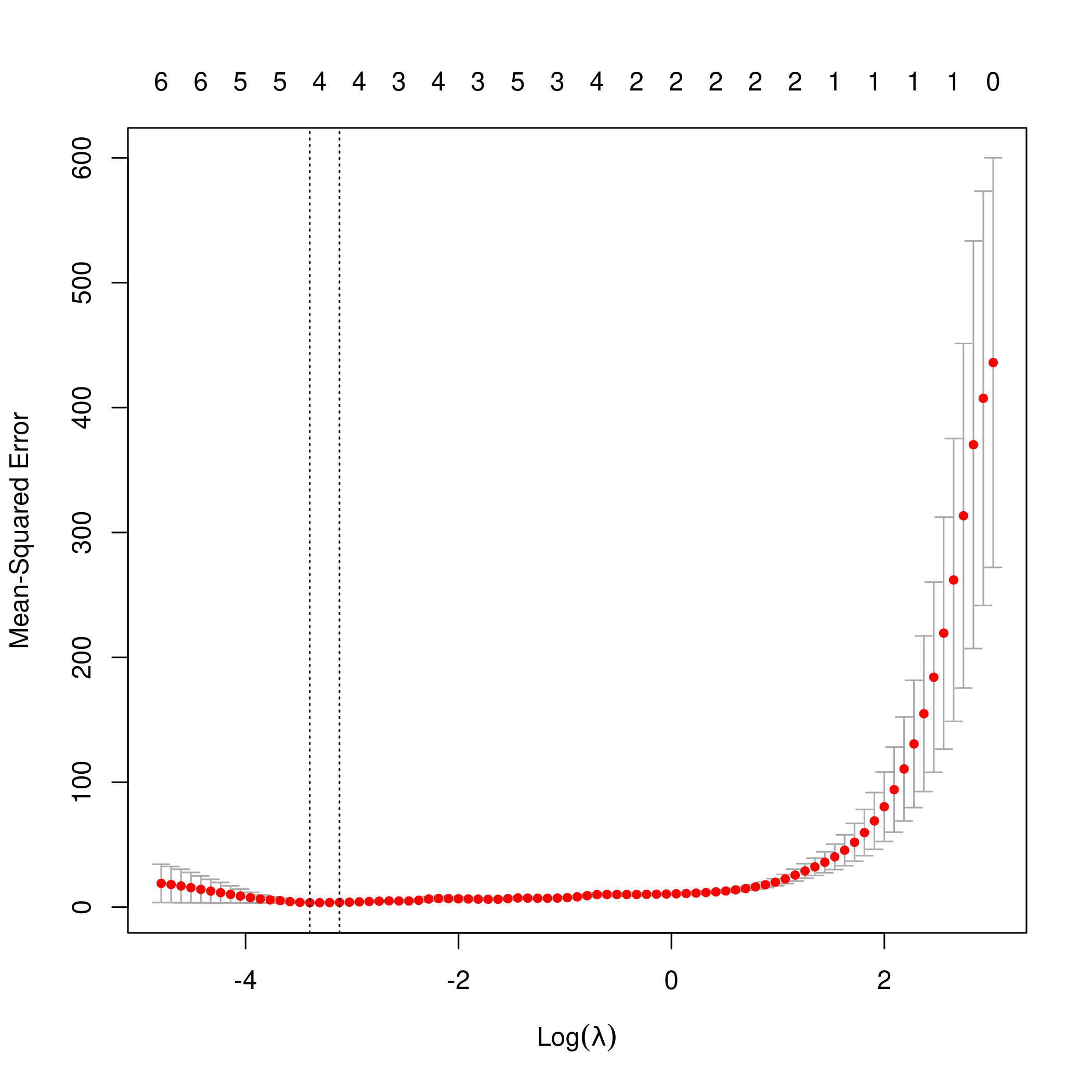
1library(glmnet)
2library(boot)
3lasso.mod2 <- cv.glmnet(as.matrix(newDF[-1]), y, alpha=1)
4lambda2 <- lasso.mod2$lambda.min
5plot(lasso.mod2)
1predict(lasso.mod2, s=lambda, type="coefficients")
1## 11 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) 42.67982691
4## x.2 3.22521396
5## x.3 8.56699146
6## x.4 .
7## x.5 -0.10229572
8## x.6 .
9## x.7 -0.03184905
10## x.8 .
11## x.9 .
12## x.10 .
13## y .
1lambda<-10^seq(-3, 3, length = 100)
2lassocaret2= train(y~.,data=newDF,method="glmnet",tuneGrid=expand.grid(alpha=1,lambda=lambda))
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1lassocaret2 %>% print
1## glmnet
2##
3## 100 samples
4## 10 predictor
5##
6## No pre-processing
7## Resampling: Bootstrapped (25 reps)
8## Summary of sample sizes: 100, 100, 100, 100, 100, 100, ...
9## Resampling results across tuning parameters:
10##
11## lambda RMSE Rsquared MAE
12## 1.000000e-03 40.03231 0.9999955 14.48774
13## 1.149757e-03 40.03231 0.9999955 14.48774
14## 1.321941e-03 40.03231 0.9999955 14.48774
15## 1.519911e-03 40.03231 0.9999955 14.48774
16## 1.747528e-03 40.03231 0.9999955 14.48774
17## 2.009233e-03 40.03231 0.9999955 14.48774
18## 2.310130e-03 40.03231 0.9999955 14.48774
19## 2.656088e-03 40.03231 0.9999955 14.48774
20## 3.053856e-03 40.03231 0.9999955 14.48774
21## 3.511192e-03 40.03231 0.9999955 14.48774
22## 4.037017e-03 40.03231 0.9999955 14.48774
23## 4.641589e-03 40.03231 0.9999955 14.48774
24## 5.336699e-03 40.03231 0.9999955 14.48774
25## 6.135907e-03 40.03231 0.9999955 14.48774
26## 7.054802e-03 40.03231 0.9999955 14.48774
27## 8.111308e-03 40.03231 0.9999955 14.48774
28## 9.326033e-03 40.03231 0.9999955 14.48774
29## 1.072267e-02 40.03231 0.9999955 14.48774
30## 1.232847e-02 40.03231 0.9999955 14.48774
31## 1.417474e-02 40.03231 0.9999955 14.48774
32## 1.629751e-02 40.03231 0.9999955 14.48774
33## 1.873817e-02 40.03231 0.9999955 14.48774
34## 2.154435e-02 40.03231 0.9999955 14.48774
35## 2.477076e-02 40.03231 0.9999955 14.48774
36## 2.848036e-02 40.03231 0.9999955 14.48774
37## 3.274549e-02 40.03231 0.9999955 14.48774
38## 3.764936e-02 40.03231 0.9999955 14.48774
39## 4.328761e-02 40.03231 0.9999955 14.48774
40## 4.977024e-02 40.03231 0.9999955 14.48774
41## 5.722368e-02 40.03231 0.9999955 14.48774
42## 6.579332e-02 40.03231 0.9999955 14.48774
43## 7.564633e-02 40.03231 0.9999955 14.48774
44## 8.697490e-02 40.03231 0.9999955 14.48774
45## 1.000000e-01 40.03231 0.9999955 14.48774
46## 1.149757e-01 40.03231 0.9999955 14.48774
47## 1.321941e-01 40.03231 0.9999955 14.48774
48## 1.519911e-01 40.03231 0.9999955 14.48774
49## 1.747528e-01 40.03231 0.9999955 14.48774
50## 2.009233e-01 40.03231 0.9999955 14.48774
51## 2.310130e-01 40.03231 0.9999955 14.48774
52## 2.656088e-01 40.03231 0.9999955 14.48774
53## 3.053856e-01 40.03231 0.9999955 14.48774
54## 3.511192e-01 40.03231 0.9999955 14.48774
55## 4.037017e-01 40.03231 0.9999955 14.48774
56## 4.641589e-01 40.03231 0.9999955 14.48774
57## 5.336699e-01 40.03231 0.9999955 14.48774
58## 6.135907e-01 40.03231 0.9999955 14.48774
59## 7.054802e-01 40.03231 0.9999955 14.48774
60## 8.111308e-01 40.03231 0.9999955 14.48774
61## 9.326033e-01 40.03231 0.9999955 14.48774
62## 1.072267e+00 40.03231 0.9999955 14.48774
63## 1.232847e+00 40.03231 0.9999955 14.48774
64## 1.417474e+00 40.03231 0.9999955 14.48774
65## 1.629751e+00 40.03231 0.9999955 14.48774
66## 1.873817e+00 40.03231 0.9999955 14.48774
67## 2.154435e+00 40.03231 0.9999955 14.48774
68## 2.477076e+00 40.03231 0.9999955 14.48774
69## 2.848036e+00 40.03231 0.9999955 14.48774
70## 3.274549e+00 40.03231 0.9999955 14.48774
71## 3.764936e+00 40.03231 0.9999955 14.48774
72## 4.328761e+00 40.03231 0.9999955 14.48774
73## 4.977024e+00 40.03231 0.9999955 14.48774
74## 5.722368e+00 40.03231 0.9999955 14.48774
75## 6.579332e+00 40.03231 0.9999955 14.48774
76## 7.564633e+00 40.43005 0.9999955 14.59881
77## 8.697490e+00 41.25214 0.9999955 14.81913
78## 1.000000e+01 42.30446 0.9999955 15.09937
79## 1.149757e+01 43.59429 0.9999955 15.44307
80## 1.321941e+01 45.43633 0.9999955 15.93255
81## 1.519911e+01 47.55425 0.9999955 16.49605
82## 1.747528e+01 49.98935 0.9999955 17.14447
83## 2.009233e+01 52.90533 0.9999955 17.91650
84## 2.310130e+01 57.57589 0.9999955 19.10125
85## 2.656088e+01 63.25484 0.9999955 20.53147
86## 3.053856e+01 70.51580 0.9999955 22.36400
87## 3.511192e+01 78.93391 0.9999955 24.49105
88## 4.037017e+01 88.61274 0.9999955 26.93830
89## 4.641589e+01 99.97831 0.9999955 29.83601
90## 5.336699e+01 113.48225 0.9999955 33.39320
91## 6.135907e+01 129.17536 0.9999955 37.58303
92## 7.054802e+01 147.76452 0.9999957 42.74333
93## 8.111308e+01 169.60027 0.9999961 48.98043
94## 9.326033e+01 194.94266 0.9999965 56.29001
95## 1.072267e+02 224.07631 0.9999969 64.70026
96## 1.232847e+02 257.56092 0.9999971 74.36989
97## 1.417474e+02 296.13382 0.9999971 85.51504
98## 1.629751e+02 340.49129 0.9999971 98.33212
99## 1.873817e+02 391.49185 0.9999971 113.06864
100## 2.154435e+02 450.13031 0.9999971 130.01206
101## 2.477076e+02 509.28329 0.9999970 147.15405
102## 2.848036e+02 564.17558 0.9999969 163.34475
103## 3.274549e+02 618.84080 0.9999969 179.85589
104## 3.764936e+02 681.69265 0.9999969 198.83969
105## 4.328761e+02 741.14452 0.9999967 217.28049
106## 4.977024e+02 807.25385 0.9999967 237.88938
107## 5.722368e+02 883.26360 0.9999967 261.58461
108## 6.579332e+02 970.65640 0.9999967 288.82836
109## 7.564633e+02 1037.84801 0.9999960 312.54099
110## 8.697490e+02 1088.92551 0.9999960 334.04769
111## 1.000000e+03 1131.46176 0.9999955 354.62317
112##
113## Tuning parameter 'alpha' was held constant at a value of 1
114## RMSE was used to select the optimal model using the smallest value.
115## The final values used for the model were alpha = 1 and lambda = 6.579332.
1lassocaret2 %>% ggplot
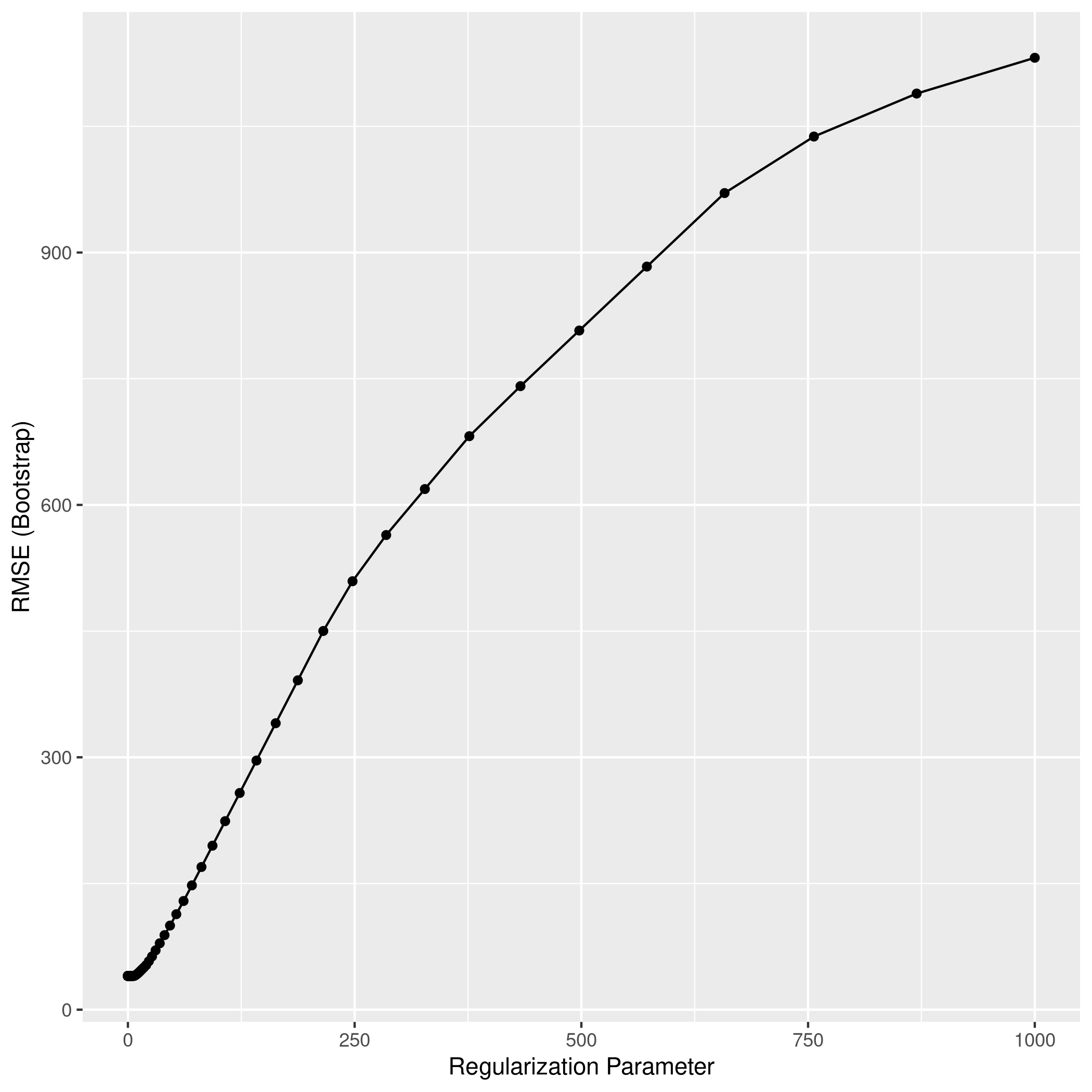
1lassocaret2 %>% varImp %>% ggplot
Clearly, the LASSO model has correctly reduced the model down to the correct single variable form, though best subset seems to suggest using more predictors, their coefficients are low enough to recognize that they are noise.
Question 6.9 - Page 263
In this exercise, we will predict the number of applications received
using the other variables in the College data set.
(a) Split the data set into a training set and a test set.
(b) Fit a linear model using least squares on the training set, and report the test error obtained.
(c) Fit a ridge regression model on the training set, with \(\lambda\) chosen by cross-validation. Report the test error obtained.
(d) Fit a lasso model on the training set, with \(\lambda\) chosen by crossvalidation. Report the test error obtained, along with the number of non-zero coefficient estimates.
(e) Fit a PCR model on the training set, with \(M\) chosen by crossvalidation. Report the test error obtained, along with the value of \(M\) selected by cross-validation.
(f) Fit a PLS model on the training set, with M chosen by crossvalidation. Report the test error obtained, along with the value of M selected by cross-validation.
(g) Comment on the results obtained. How accurately can we predict the number of college applications received? Is there much difference among the test errors resulting from these five approaches?
Answer
We will use the caret package, since at the moment, mlr3 does not
have learners for PCR and PLS.
1colDat<-ISLR::College
2colDat %>% summary %>% print
1## Private Apps Accept Enroll Top10perc
2## No :212 Min. : 81 Min. : 72 Min. : 35 Min. : 1.00
3## Yes:565 1st Qu.: 776 1st Qu.: 604 1st Qu.: 242 1st Qu.:15.00
4## Median : 1558 Median : 1110 Median : 434 Median :23.00
5## Mean : 3002 Mean : 2019 Mean : 780 Mean :27.56
6## 3rd Qu.: 3624 3rd Qu.: 2424 3rd Qu.: 902 3rd Qu.:35.00
7## Max. :48094 Max. :26330 Max. :6392 Max. :96.00
8## Top25perc F.Undergrad P.Undergrad Outstate
9## Min. : 9.0 Min. : 139 Min. : 1.0 Min. : 2340
10## 1st Qu.: 41.0 1st Qu.: 992 1st Qu.: 95.0 1st Qu.: 7320
11## Median : 54.0 Median : 1707 Median : 353.0 Median : 9990
12## Mean : 55.8 Mean : 3700 Mean : 855.3 Mean :10441
13## 3rd Qu.: 69.0 3rd Qu.: 4005 3rd Qu.: 967.0 3rd Qu.:12925
14## Max. :100.0 Max. :31643 Max. :21836.0 Max. :21700
15## Room.Board Books Personal PhD
16## Min. :1780 Min. : 96.0 Min. : 250 Min. : 8.00
17## 1st Qu.:3597 1st Qu.: 470.0 1st Qu.: 850 1st Qu.: 62.00
18## Median :4200 Median : 500.0 Median :1200 Median : 75.00
19## Mean :4358 Mean : 549.4 Mean :1341 Mean : 72.66
20## 3rd Qu.:5050 3rd Qu.: 600.0 3rd Qu.:1700 3rd Qu.: 85.00
21## Max. :8124 Max. :2340.0 Max. :6800 Max. :103.00
22## Terminal S.F.Ratio perc.alumni Expend
23## Min. : 24.0 Min. : 2.50 Min. : 0.00 Min. : 3186
24## 1st Qu.: 71.0 1st Qu.:11.50 1st Qu.:13.00 1st Qu.: 6751
25## Median : 82.0 Median :13.60 Median :21.00 Median : 8377
26## Mean : 79.7 Mean :14.09 Mean :22.74 Mean : 9660
27## 3rd Qu.: 92.0 3rd Qu.:16.50 3rd Qu.:31.00 3rd Qu.:10830
28## Max. :100.0 Max. :39.80 Max. :64.00 Max. :56233
29## Grad.Rate
30## Min. : 10.00
31## 1st Qu.: 53.00
32## Median : 65.00
33## Mean : 65.46
34## 3rd Qu.: 78.00
35## Max. :118.00
1colDat %>% str %>% print
1## 'data.frame': 777 obs. of 18 variables:
2## $ Private : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 2 2 2 2 2 ...
3## $ Apps : num 1660 2186 1428 417 193 ...
4## $ Accept : num 1232 1924 1097 349 146 ...
5## $ Enroll : num 721 512 336 137 55 158 103 489 227 172 ...
6## $ Top10perc : num 23 16 22 60 16 38 17 37 30 21 ...
7## $ Top25perc : num 52 29 50 89 44 62 45 68 63 44 ...
8## $ F.Undergrad: num 2885 2683 1036 510 249 ...
9## $ P.Undergrad: num 537 1227 99 63 869 ...
10## $ Outstate : num 7440 12280 11250 12960 7560 ...
11## $ Room.Board : num 3300 6450 3750 5450 4120 ...
12## $ Books : num 450 750 400 450 800 500 500 450 300 660 ...
13## $ Personal : num 2200 1500 1165 875 1500 ...
14## $ PhD : num 70 29 53 92 76 67 90 89 79 40 ...
15## $ Terminal : num 78 30 66 97 72 73 93 100 84 41 ...
16## $ S.F.Ratio : num 18.1 12.2 12.9 7.7 11.9 9.4 11.5 13.7 11.3 11.5 ...
17## $ perc.alumni: num 12 16 30 37 2 11 26 37 23 15 ...
18## $ Expend : num 7041 10527 8735 19016 10922 ...
19## $ Grad.Rate : num 60 56 54 59 15 55 63 73 80 52 ...
20## NULL
1colDat %>% sapply(unique) %>% sapply(length) %>% print
1## Private Apps Accept Enroll Top10perc Top25perc
2## 2 711 693 581 82 89
3## F.Undergrad P.Undergrad Outstate Room.Board Books Personal
4## 714 566 640 553 122 294
5## PhD Terminal S.F.Ratio perc.alumni Expend Grad.Rate
6## 78 65 173 61 744 81
Clearly, there are no psuedo-factors which might have been converted at this stage.
a) Train-Test split
1train_ind<-createDataPartition(colDat$Apps,p=0.8,times=1,list=FALSE)
2train_set<-colDat[train_ind,]
3test_set<-colDat[-train_ind,]
b) Linear least squares
1linCol<-train(Apps~.,data=train_set,method="lm")
2linCol %>% summary
1##
2## Call:
3## lm(formula = .outcome ~ ., data = dat)
4##
5## Residuals:
6## Min 1Q Median 3Q Max
7## -5145.6 -414.8 -20.3 340.5 7526.8
8##
9## Coefficients:
10## Estimate Std. Error t value Pr(>|t|)
11## (Intercept) -2.918e+02 4.506e+02 -0.648 0.517486
12## PrivateYes -5.351e+02 1.532e+02 -3.494 0.000511 ***
13## Accept 1.617e+00 4.258e-02 37.983 < 2e-16 ***
14## Enroll -1.012e+00 1.959e-01 -5.165 3.26e-07 ***
15## Top10perc 5.379e+01 6.221e+00 8.647 < 2e-16 ***
16## Top25perc -1.632e+01 5.046e+00 -3.235 0.001282 **
17## F.Undergrad 6.836e-02 3.457e-02 1.978 0.048410 *
18## P.Undergrad 7.929e-02 3.367e-02 2.355 0.018854 *
19## Outstate -7.303e-02 2.098e-02 -3.481 0.000536 ***
20## Room.Board 1.695e-01 5.367e-02 3.159 0.001663 **
21## Books 9.998e-02 2.578e-01 0.388 0.698328
22## Personal -3.145e-03 6.880e-02 -0.046 0.963553
23## PhD -8.926e+00 5.041e+00 -1.771 0.077112 .
24## Terminal -2.298e+00 5.608e+00 -0.410 0.682152
25## S.F.Ratio 6.038e+00 1.420e+01 0.425 0.670757
26## perc.alumni -5.085e-01 4.560e+00 -0.112 0.911249
27## Expend 4.668e-02 1.332e-02 3.505 0.000490 ***
28## Grad.Rate 9.042e+00 3.379e+00 2.676 0.007653 **
29## ---
30## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
31##
32## Residual standard error: 1042 on 606 degrees of freedom
33## Multiple R-squared: 0.9332, Adjusted R-squared: 0.9313
34## F-statistic: 497.7 on 17 and 606 DF, p-value: < 2.2e-16
1linPred<-predict(linCol,test_set)
2linPred %>% postResample(obs = test_set$Apps)
1## RMSE Rsquared MAE
2## 1071.6360025 0.9017032 625.7827996
Do note that the metrics are calculated in a manner to ensure no negative values are obtained.
c) Ridge regression with CV for λ
1L2Grid <- expand.grid(alpha=0,
2 lambda=10^seq(from=-3,to=30,length=100))
1ridgCol<-train(Apps~.,data=train_set,method="glmnet",tuneGrid = L2Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1ridgCol %>% summary %>% print
1## Length Class Mode
2## a0 100 -none- numeric
3## beta 1700 dgCMatrix S4
4## df 100 -none- numeric
5## dim 2 -none- numeric
6## lambda 100 -none- numeric
7## dev.ratio 100 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 17 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(ridgCol$finalModel, ridgCol$bestTune$lambda) %>% print
1## 18 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) -1.407775e+03
4## PrivateYes -5.854245e+02
5## Accept 1.042778e+00
6## Enroll 3.511219e-01
7## Top10perc 2.780211e+01
8## Top25perc 2.883536e-02
9## F.Undergrad 6.825141e-02
10## P.Undergrad 5.281320e-02
11## Outstate -2.011504e-02
12## Room.Board 2.155224e-01
13## Books 1.517585e-01
14## Personal -3.711406e-02
15## PhD -4.453155e+00
16## Terminal -3.783231e+00
17## S.F.Ratio 6.897360e+00
18## perc.alumni -9.301831e+00
19## Expend 5.601144e-02
20## Grad.Rate 1.259989e+01
1ggplot(ridgCol)
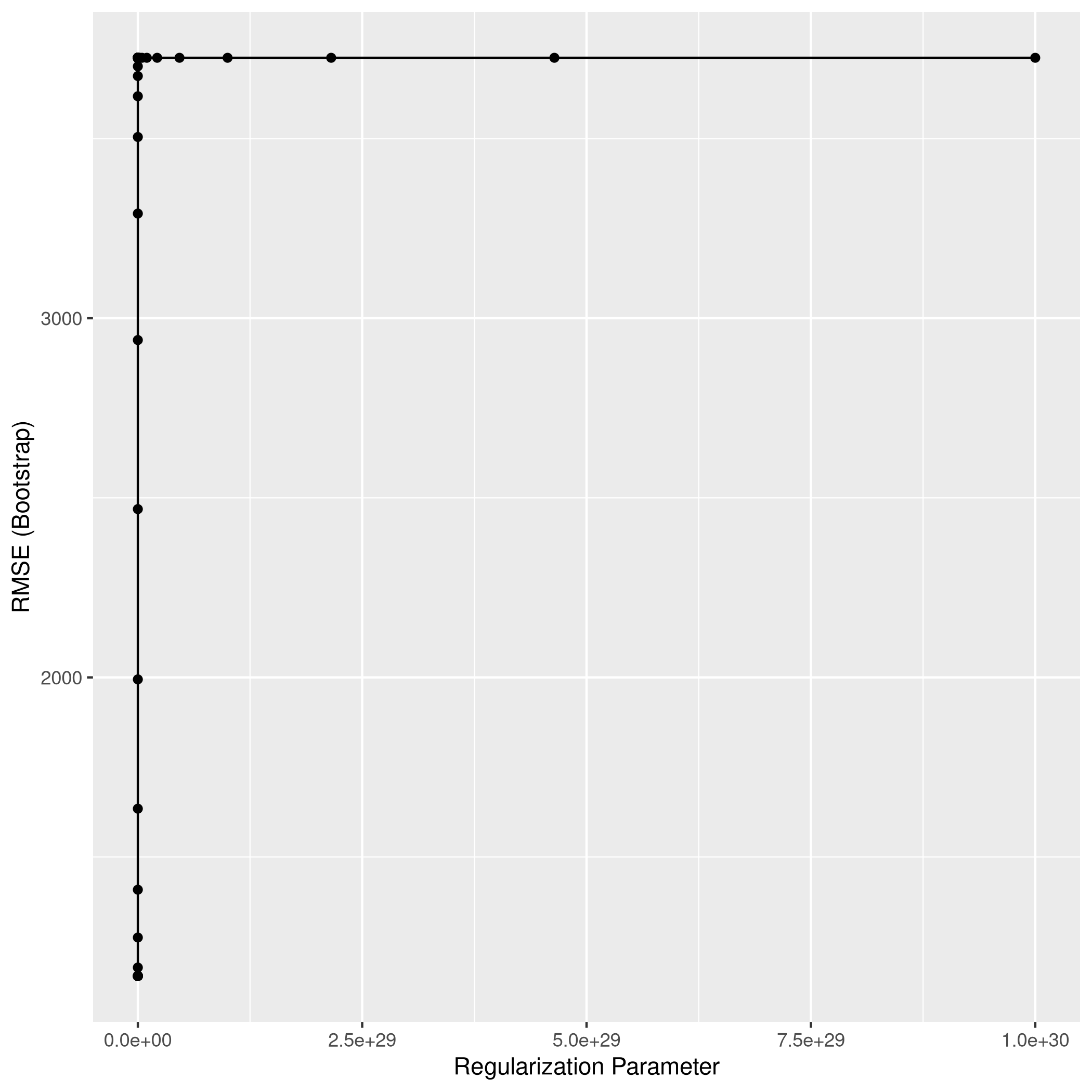
1ridgPred<-predict(ridgCol,test_set)
2ridgPred %>% postResample(obs = test_set$Apps)
1## RMSE Rsquared MAE
2## 1047.7545250 0.9051726 644.4535063
d) LASSO with CV for λ
1L1Grid <- expand.grid(alpha=1, # for lasso
2 lambda=10^seq(from=-3,to=30,length=100))
1lassoCol<-train(Apps~.,data=train_set,method="glmnet",tuneGrid = L1Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1lassoCol %>% summary %>% print
1## Length Class Mode
2## a0 81 -none- numeric
3## beta 1377 dgCMatrix S4
4## df 81 -none- numeric
5## dim 2 -none- numeric
6## lambda 81 -none- numeric
7## dev.ratio 81 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 17 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(lassoCol$finalModel, lassoCol$bestTune$lambda) %>% print
1## 18 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) -325.51554340
4## PrivateYes -532.28956305
5## Accept 1.60370798
6## Enroll -0.90158328
7## Top10perc 51.96610325
8## Top25perc -14.87886847
9## F.Undergrad 0.05352324
10## P.Undergrad 0.07832395
11## Outstate -0.07047302
12## Room.Board 0.16783269
13## Books 0.08836704
14## Personal .
15## PhD -8.67634519
16## Terminal -2.18494018
17## S.F.Ratio 5.25050018
18## perc.alumni -0.67848535
19## Expend 0.04597728
20## Grad.Rate 8.67569015
1ggplot(lassoCol)
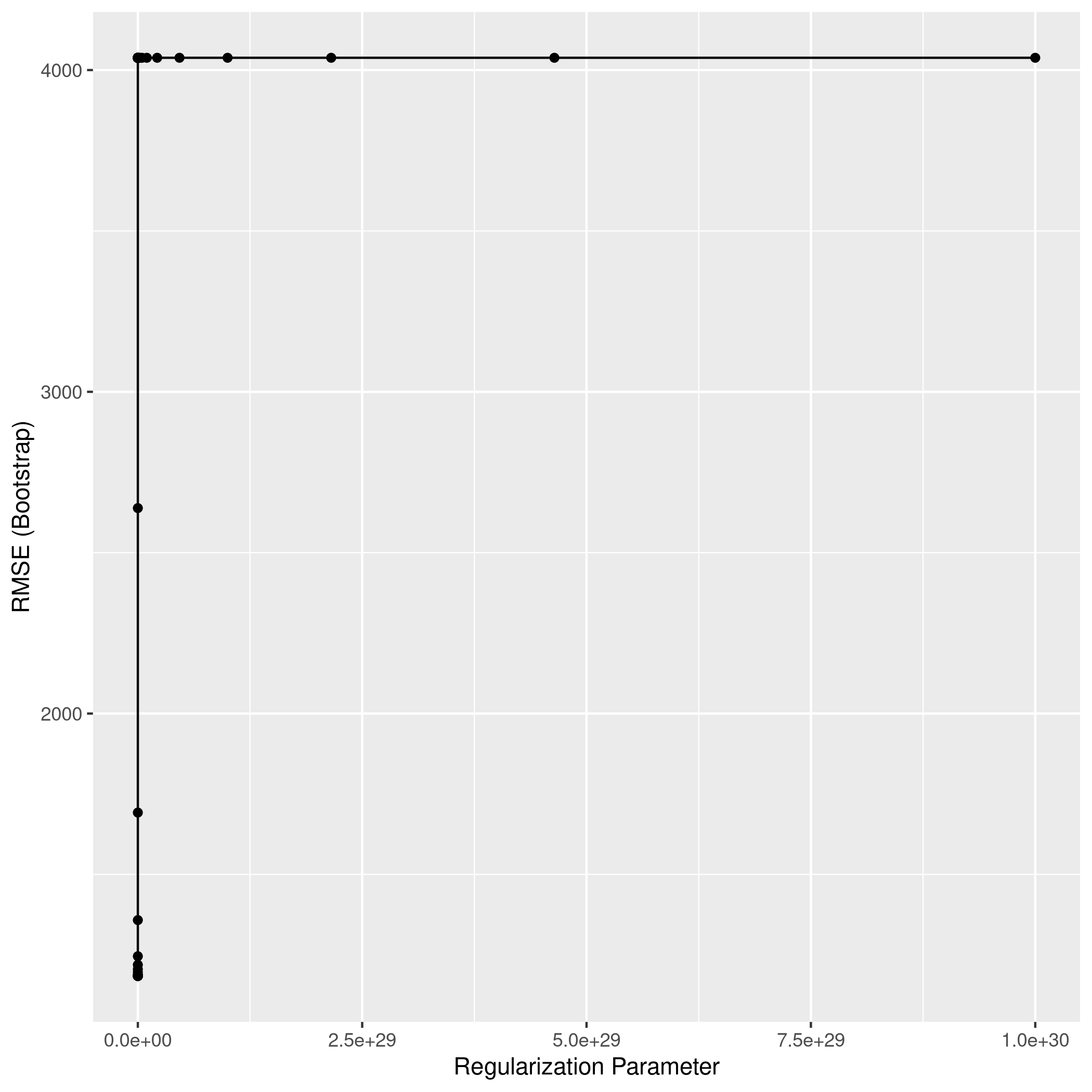
1lassoPred<-predict(lassoCol,test_set)
2lassoPred %>% postResample(obs = test_set$Apps)
1## RMSE Rsquared MAE
2## 1068.9834769 0.9021268 622.7029418
e) PCR with CV for M
1mGrid <- expand.grid(ncomp=seq(from=1,to=20,length=10))
1pcrCol<-train(Apps~.,data=train_set,method="pcr",tuneGrid = mGrid)
2pcrCol %>% summary %>% print
1## Data: X dimension: 624 17
2## Y dimension: 624 1
3## Fit method: svdpc
4## Number of components considered: 17
5## TRAINING: % variance explained
6## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
7## X 48.2314 87.24 95.02 97.26 98.63 99.43 99.91
8## .outcome 0.2419 76.54 77.88 80.19 91.27 91.34 91.34
9## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
10## X 99.96 100.00 100.00 100.00 100.00 100.00 100.00
11## .outcome 91.65 91.66 92.26 92.65 92.66 92.67 92.76
12## 15 comps 16 comps 17 comps
13## X 100.00 100.00 100.00
14## .outcome 93.17 93.18 93.32
15## NULL
1ggplot(pcrCol)
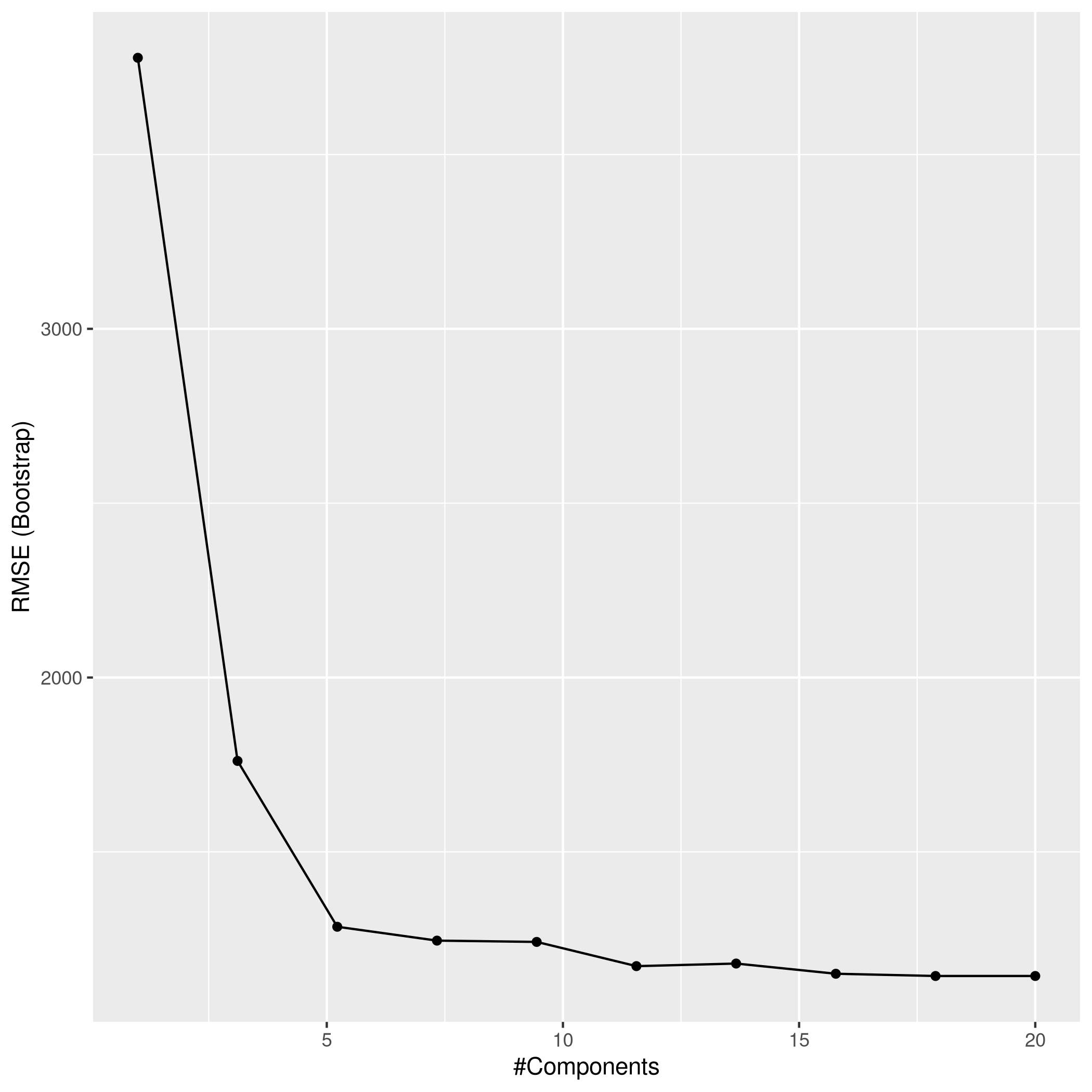
1pcrPred<-predict(pcrCol,test_set)
2pcrPred %>% postResample(obs = test_set$Apps)
1## RMSE Rsquared MAE
2## 1071.6360025 0.9017032 625.7827996
f) PLS with CV for M
1plsCol<-train(Apps~.,data=train_set,method="pls",tuneGrid = mGrid)
2plsCol %>% summary %>% print
1## Data: X dimension: 624 17
2## Y dimension: 624 1
3## Fit method: oscorespls
4## Number of components considered: 17
5## TRAINING: % variance explained
6## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
7## X 39.02 56.4 91.83 96.61 98.62 99.22 99.49
8## .outcome 78.04 84.1 86.88 91.09 91.38 91.49 91.66
9## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
10## X 99.96 99.99 100.00 100.00 100.00 100.00 100.00
11## .outcome 91.68 91.85 92.64 92.87 93.16 93.18 93.18
12## 15 comps 16 comps 17 comps
13## X 100.00 100.00 100.00
14## .outcome 93.18 93.19 93.32
15## NULL
1ggplot(plsCol)
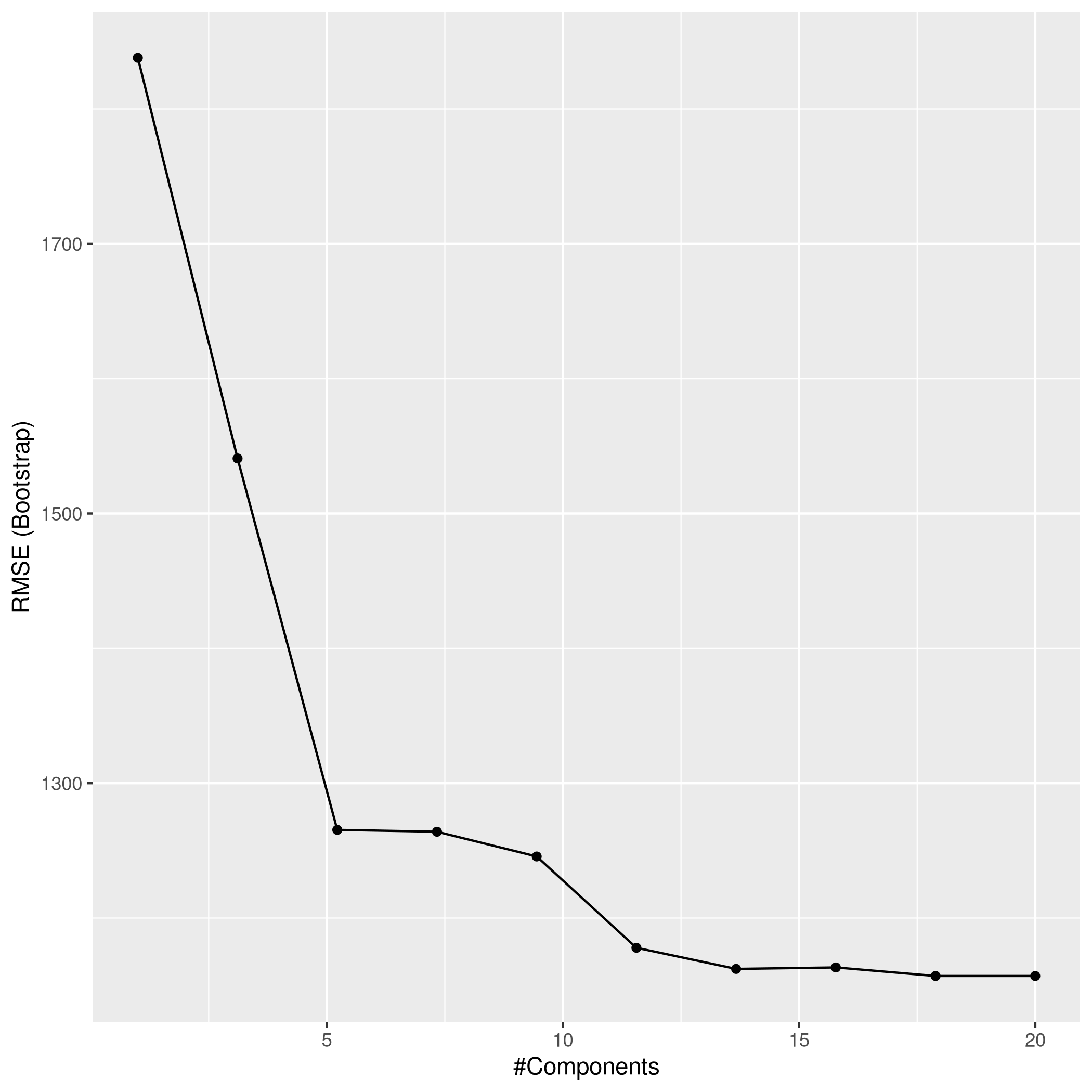
1plsPred<-predict(plsCol,test_set)
2plsPred %>% postResample(obs = test_set$Apps)
1## RMSE Rsquared MAE
2## 1071.6360039 0.9017032 625.7827987
g) Comments and Comparison
1models <- list(ridge = ridgCol, lasso = lassoCol, pcr = pcrCol, pls=plsCol,linear=linCol)
2resamples(models) %>% summary
1##
2## Call:
3## summary.resamples(object = .)
4##
5## Models: ridge, lasso, pcr, pls, linear
6## Number of resamples: 25
7##
8## MAE
9## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
10## ridge 536.9612 600.5398 623.2005 649.6713 707.4014 793.4972 0
11## lasso 573.8563 616.3883 671.9453 655.8858 691.7620 732.2155 0
12## pcr 576.1427 618.8694 650.0360 662.9040 714.8491 767.5535 0
13## pls 553.3999 607.9757 637.1985 638.6619 668.5120 735.4479 0
14## linear 556.5553 619.2395 654.1478 659.4635 686.7747 792.4912 0
15##
16## RMSE
17## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
18## ridge 882.2646 920.5934 1000.519 1168.603 1163.377 1939.541 0
19## lasso 801.9415 990.0724 1168.234 1184.329 1302.221 1584.712 0
20## pcr 828.1370 942.2678 1131.207 1144.071 1284.178 1544.078 0
21## pls 786.7989 1038.3265 1167.764 1157.026 1274.041 1461.434 0
22## linear 798.3771 1063.3690 1134.291 1135.977 1215.115 1403.576 0
23##
24## Rsquared
25## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
26## ridge 0.8735756 0.8962010 0.9185736 0.9136429 0.9306819 0.9474913 0
27## lasso 0.8851991 0.9132766 0.9217660 0.9191638 0.9284838 0.9398772 0
28## pcr 0.8658504 0.9080179 0.9235117 0.9146884 0.9281892 0.9471991 0
29## pls 0.8881249 0.9080786 0.9183968 0.9173632 0.9258994 0.9420894 0
30## linear 0.8840049 0.8986452 0.9222319 0.9160913 0.9296275 0.9492198 0
1resamples(models) %>% bwplot(scales="free")
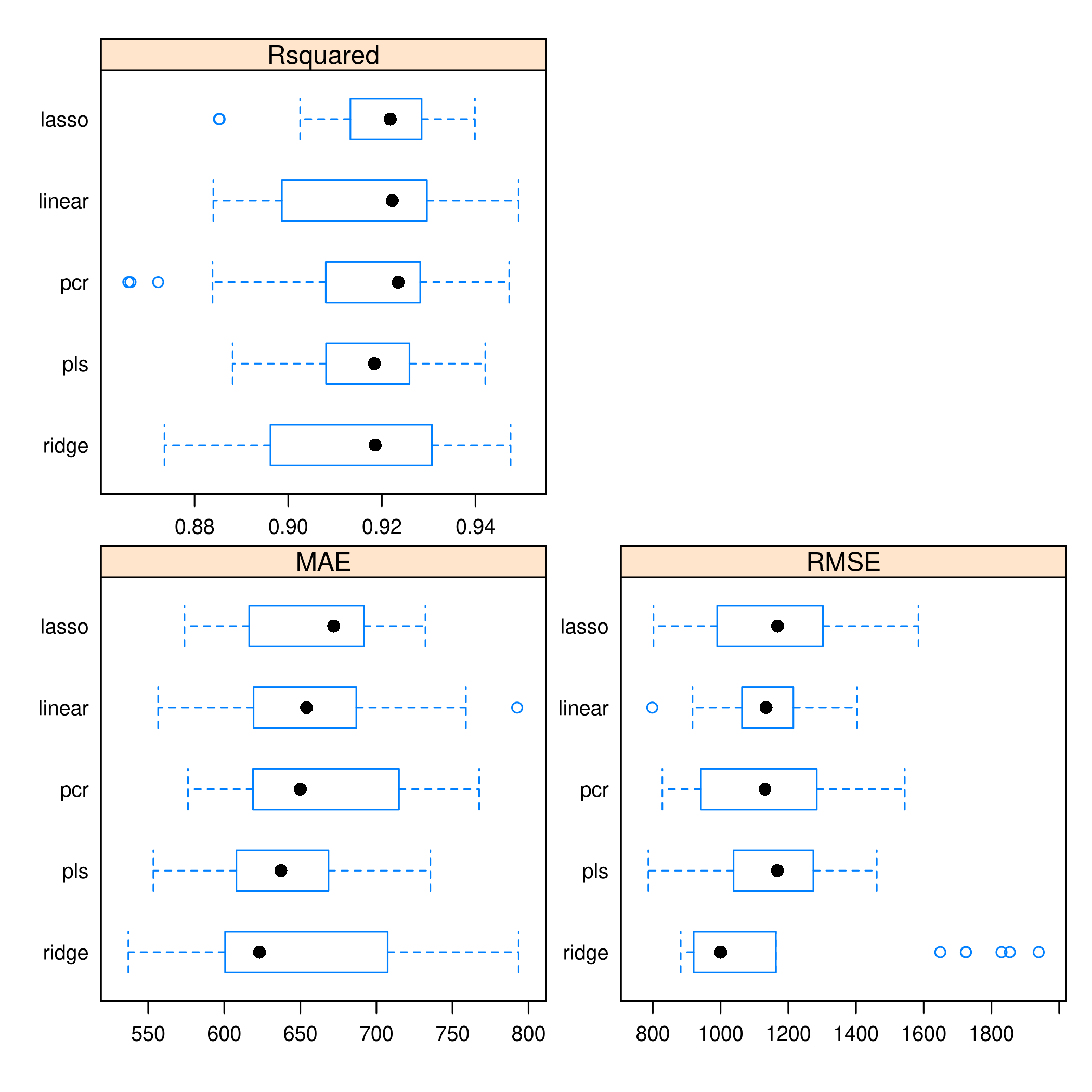
- Given the tighter spread of
PLS, it seems more reliable thanPCR Ridgeis just poor in every wayOLSdoes well, but it also has a worrying outlierLASSOappears to be doing alright as well We also have kept track of the performance on thetest_set
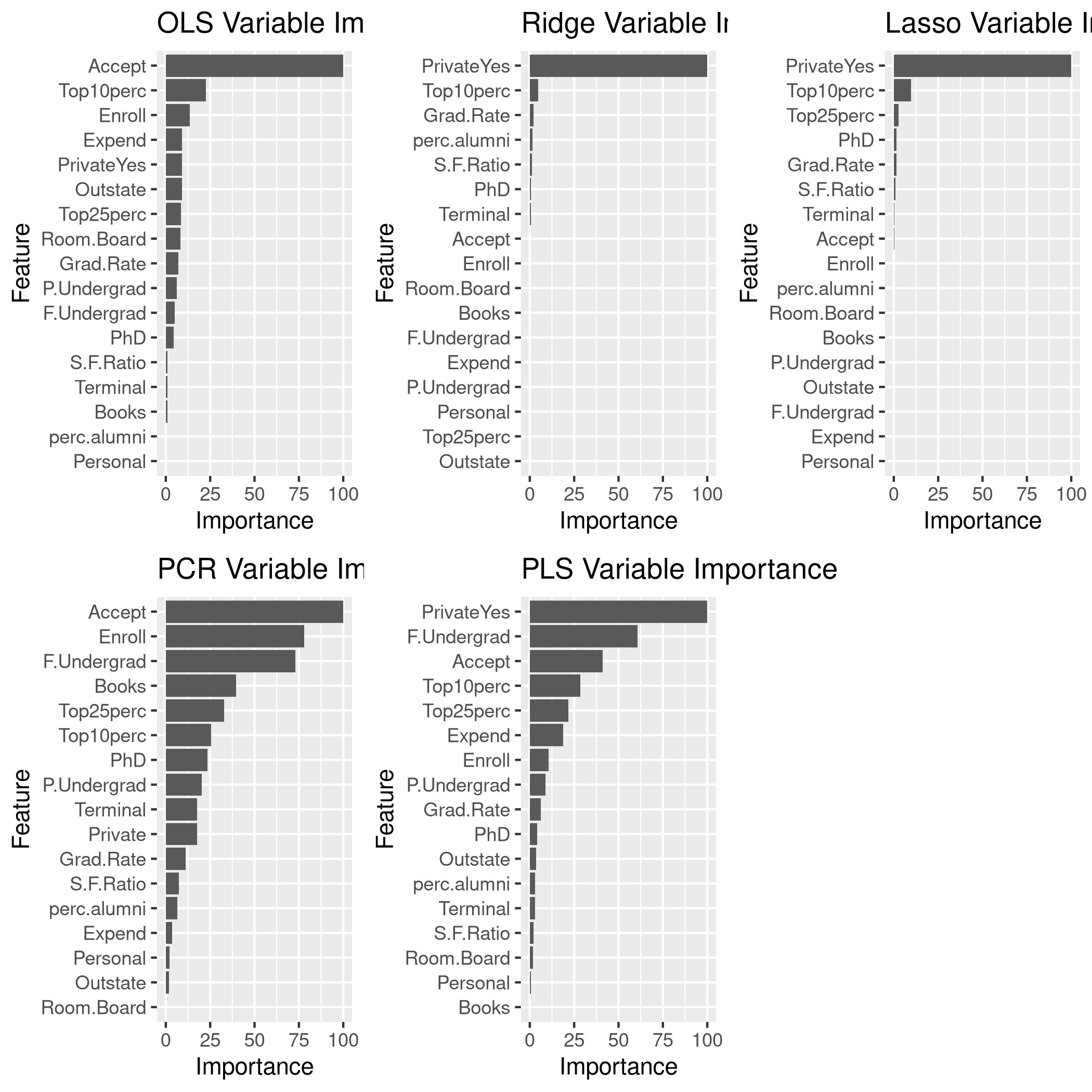
We might want to see the variable significance values as well.
1lgp<-linCol %>% varImp %>% ggplot + ggtitle("OLS Variable Importance")
2rgp<-ridgCol %>% varImp %>% ggplot + ggtitle("Ridge Variable Importance")
3lsgp<-lassoCol %>% varImp %>% ggplot + ggtitle("Lasso Variable Importance")
4pcgp<-pcrCol %>% varImp %>% ggplot + ggtitle("PCR Variable Importance")
5plgp<-plsCol %>% varImp %>% ggplot + ggtitle("PLS Variable Importance")
6grid.arrange(lgp,rgp,lsgp,pcgp,plgp,ncol=3)
Question 6.10 - Pages 263-264
We have seen that as the number of features used in a model increases, the training error will necessarily decrease, but the test error may not. We will now explore this in a simulated data set.
(a) Generate a data set with \(p = 20\) features, \(n = 1,000\) observations, and an associated quantitative response vector generated according to the model \[Y = X\beta + \eta,\] where \(\beta\) has some elements that are exactly equal to zero.
(b) Split your data set into a training set containing \(100\) observations and a test set containing \(900\) observations.
(c) Perform best subset selection on the training set, and plot the training set MSE associated with the best model of each size.
(d) Plot the test set MSE associated with the best model of each size.
(e) For which model size does the test set MSE take on its minimum value? Comment on your results. If it takes on its minimum value for a model containing only an intercept or a model containing all of the features, then play around with the way that you are generating the data in (a) until you come up with a scenario in which the test set MSE is minimized for an intermediate model size.
(f) How does the model at which the test set MSE is minimized compare to the true model used to generate the data? Comment on the coefficient values.
(g) Create a plot displaying \(\sqrt{\Sum_{j=1}^{p}(\beta_{j}-\hat{\beta}_{j}^{r})^{2}}\) for a range of values of \(r\), where \(\hat{\beta}_{j}^{r}\) is the $j$th coefficient estimate for the best model containing \(r\) coefficients. Comment on what you observe. How does this compare to the test MSE plot from (d)?
Answer
Model creation
1p=20
2n=1000
3noise<-rnorm(n)
4xmat<-matrix(rnorm(n*p),nrow=n,ncol=p)
5beta<-sample(-10:34,20)
6beta[sample(1:20,4)]=0
7myY<-xmat %*% beta + noise
8modelDat<-data.frame(x=as.matrix(xmat),y=myY)
- As always we will want to take a peak
1modelDat %>% str %>% print
1## 'data.frame': 1000 obs. of 21 variables:
2## $ x.1 : num -0.406 -1.375 0.858 -0.231 -0.601 ...
3## $ x.2 : num -0.129 -0.218 -0.17 0.573 -0.513 ...
4## $ x.3 : num 0.127 -0.224 1.014 0.896 0.159 ...
5## $ x.4 : num 0.499 -0.151 -0.488 -0.959 2.187 ...
6## $ x.5 : num -0.235 -0.345 -0.773 -0.346 0.773 ...
7## $ x.6 : num 0.26 -0.429 -1.183 -1.159 0.959 ...
8## $ x.7 : num 0.567 1.647 0.149 -0.593 -0.902 ...
9## $ x.8 : num -0.092 0.8391 -1.4835 0.0229 -0.1353 ...
10## $ x.9 : num -0.998 -1.043 -0.563 -0.377 0.324 ...
11## $ x.10: num -0.4401 -0.195 -0.5139 -0.0156 -0.9543 ...
12## $ x.11: num -0.147 0.829 0.165 0.101 -0.105 ...
13## $ x.12: num -0.0118 1.02 1.0794 1.3184 -2.2844 ...
14## $ x.13: num -1.683 0.487 -1.142 -0.744 -0.175 ...
15## $ x.14: num 0.228 -1.031 -2.798 -0.646 0.56 ...
16## $ x.15: num -0.718 0.508 0.637 -0.556 0.585 ...
17## $ x.16: num -1.6378 0.581 -0.9939 0.0537 -0.5854 ...
18## $ x.17: num 1.758 -0.616 1.377 -0.876 -1.174 ...
19## $ x.18: num -1.438 0.373 1.364 0.399 0.949 ...
20## $ x.19: num -0.715 -0.731 1.142 0.149 0.916 ...
21## $ x.20: num 2.774 -2.024 1.316 0.138 0.187 ...
22## $ y : num 77.5 -82.8 -38.9 -79.7 64.9 ...
23## NULL
1modelDat %>% summary %>% print
1## x.1 x.2 x.3 x.4
2## Min. :-2.79766 Min. :-3.13281 Min. :-2.71232 Min. :-4.29604
3## 1st Qu.:-0.60516 1st Qu.:-0.66759 1st Qu.:-0.60561 1st Qu.:-0.66598
4## Median : 0.04323 Median : 0.03681 Median : 0.06556 Median : 0.06589
5## Mean : 0.06879 Mean : 0.01004 Mean : 0.06443 Mean : 0.02244
6## 3rd Qu.: 0.74049 3rd Qu.: 0.68234 3rd Qu.: 0.70521 3rd Qu.: 0.71174
7## Max. : 3.50354 Max. : 3.47268 Max. : 3.02817 Max. : 3.27326
8## x.5 x.6 x.7 x.8
9## Min. :-3.228376 Min. :-4.24014 Min. :-2.98577 Min. :-3.27770
10## 1st Qu.:-0.698220 1st Qu.:-0.69448 1st Qu.:-0.59092 1st Qu.:-0.52939
11## Median :-0.058778 Median :-0.01141 Median : 0.01732 Median : 0.05703
12## Mean : 0.000126 Mean :-0.05158 Mean : 0.04767 Mean : 0.08231
13## 3rd Qu.: 0.663570 3rd Qu.: 0.64217 3rd Qu.: 0.67438 3rd Qu.: 0.72849
14## Max. : 3.036307 Max. : 3.27572 Max. : 2.72163 Max. : 3.33409
15## x.9 x.10 x.11 x.12
16## Min. :-3.08957 Min. :-3.21268 Min. :-3.00572 Min. :-3.72016
17## 1st Qu.:-0.65456 1st Qu.:-0.69401 1st Qu.:-0.68226 1st Qu.:-0.63043
18## Median :-0.04242 Median :-0.03069 Median :-0.04777 Median : 0.07079
19## Mean : 0.02049 Mean :-0.02400 Mean :-0.03729 Mean : 0.03769
20## 3rd Qu.: 0.71209 3rd Qu.: 0.61540 3rd Qu.: 0.64873 3rd Qu.: 0.67155
21## Max. : 3.23110 Max. : 2.76059 Max. : 2.87306 Max. : 3.48569
22## x.13 x.14 x.15 x.16
23## Min. :-3.20126 Min. :-3.55432 Min. :-2.857575 Min. :-3.5383
24## 1st Qu.:-0.68535 1st Qu.:-0.66752 1st Qu.:-0.658708 1st Qu.:-0.7813
25## Median :-0.01329 Median :-0.03302 Median : 0.020581 Median :-0.0740
26## Mean : 0.01094 Mean : 0.02113 Mean : 0.007976 Mean :-0.0883
27## 3rd Qu.: 0.64877 3rd Qu.: 0.74919 3rd Qu.: 0.670464 3rd Qu.: 0.5568
28## Max. : 2.78973 Max. : 3.47923 Max. : 2.891527 Max. : 3.0938
29## x.17 x.18 x.19 x.20
30## Min. :-3.28570 Min. :-4.06416 Min. :-3.0443 Min. :-4.06307
31## 1st Qu.:-0.72302 1st Qu.:-0.72507 1st Qu.:-0.6684 1st Qu.:-0.70518
32## Median :-0.02439 Median :-0.04941 Median :-0.0610 Median :-0.07697
33## Mean :-0.01459 Mean :-0.03164 Mean :-0.0414 Mean :-0.05302
34## 3rd Qu.: 0.62692 3rd Qu.: 0.68115 3rd Qu.: 0.6381 3rd Qu.: 0.58597
35## Max. : 2.86446 Max. : 3.32958 Max. : 3.1722 Max. : 3.01358
36## y
37## Min. :-199.268
38## 1st Qu.: -54.758
39## Median : -1.607
40## Mean : -1.710
41## 3rd Qu.: 49.367
42## Max. : 278.244
b) Train Test Split
1train_ind = sample(modelDat %>% nrow,100)
2test_ind = setdiff(seq_len(modelDat %>% nrow), train_set)
Best subset selection
1train_set<-modelDat[train_ind,]
2test_set<-modelDat[-train_ind,]
1linCol<-train(y~.,data=train_set,method="lm")
2linCol %>% summary
1##
2## Call:
3## lm(formula = .outcome ~ ., data = dat)
4##
5## Residuals:
6## Min 1Q Median 3Q Max
7## -2.12474 -0.53970 -0.00944 0.42398 2.21086
8##
9## Coefficients:
10## Estimate Std. Error t value Pr(>|t|)
11## (Intercept) -0.06052 0.09604 -0.630 0.530
12## x.1 -0.02265 0.09198 -0.246 0.806
13## x.2 28.91650 0.09879 292.719 <2e-16 ***
14## x.3 14.16532 0.09343 151.610 <2e-16 ***
15## x.4 28.16256 0.09828 286.564 <2e-16 ***
16## x.5 0.13742 0.09658 1.423 0.159
17## x.6 27.01497 0.08540 316.341 <2e-16 ***
18## x.7 31.15917 0.09003 346.092 <2e-16 ***
19## x.8 -9.66308 0.11095 -87.094 <2e-16 ***
20## x.9 0.11641 0.10768 1.081 0.283
21## x.10 19.06687 0.09662 197.344 <2e-16 ***
22## x.11 -9.09956 0.08627 -105.472 <2e-16 ***
23## x.12 -8.01933 0.10198 -78.633 <2e-16 ***
24## x.13 4.26852 0.09888 43.170 <2e-16 ***
25## x.14 20.22366 0.09853 205.247 <2e-16 ***
26## x.15 -0.16607 0.10466 -1.587 0.117
27## x.16 7.95594 0.11250 70.721 <2e-16 ***
28## x.17 10.89851 0.11157 97.684 <2e-16 ***
29## x.18 -1.09760 0.09391 -11.688 <2e-16 ***
30## x.19 22.05197 0.08697 253.553 <2e-16 ***
31## x.20 20.88796 0.09274 225.221 <2e-16 ***
32## ---
33## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
34##
35## Residual standard error: 0.8583 on 79 degrees of freedom
36## Multiple R-squared: 0.9999, Adjusted R-squared: 0.9999
37## F-statistic: 4.71e+04 on 20 and 79 DF, p-value: < 2.2e-16
1linPred<-predict(linCol,test_set)
2linPred %>% postResample(obs = test_set$y)
1## RMSE Rsquared MAE
2## 1.2151815 0.9997265 0.9638378
1L2Grid <- expand.grid(alpha=0,
2 lambda=10^seq(from=-3,to=30,length=100))
1ridgCol<-train(y~.,data=train_set,method="glmnet",tuneGrid = L2Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1ridgCol %>% summary %>% print
1## Length Class Mode
2## a0 100 -none- numeric
3## beta 2000 dgCMatrix S4
4## df 100 -none- numeric
5## dim 2 -none- numeric
6## lambda 100 -none- numeric
7## dev.ratio 100 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 20 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(ridgCol$finalModel, ridgCol$bestTune$lambda) %>% print
1## 21 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) 0.03898376
4## x.1 -0.12140945
5## x.2 27.63771674
6## x.3 13.46853844
7## x.4 26.54402352
8## x.5 -0.13838118
9## x.6 25.87706885
10## x.7 29.90687677
11## x.8 -9.42088971
12## x.9 -0.08983349
13## x.10 17.45444598
14## x.11 -8.33991071
15## x.12 -7.23653865
16## x.13 3.35145521
17## x.14 19.42178898
18## x.15 -0.02794731
19## x.16 7.63951382
20## x.17 11.08083907
21## x.18 -1.36872894
22## x.19 20.90257005
23## x.20 20.07494414
1ggplot(ridgCol)
1ridgPred<-predict(ridgCol,test_set)
2ridgPred %>% postResample(obs = test_set$y)
1## RMSE Rsquared MAE
2## 3.7554417 0.9994231 3.0184859
1L1Grid <- expand.grid(alpha=1, # for lasso
2 lambda=10^seq(from=-3,to=30,length=100))
1lassoCol<-train(y~.,data=train_set,method="glmnet",tuneGrid = L1Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1lassoCol %>% summary %>% print
1## Length Class Mode
2## a0 47 -none- numeric
3## beta 940 dgCMatrix S4
4## df 47 -none- numeric
5## dim 2 -none- numeric
6## lambda 47 -none- numeric
7## dev.ratio 47 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 20 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(lassoCol$finalModel, lassoCol$bestTune$lambda) %>% print
1## 21 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) 0.1158884
4## x.1 .
5## x.2 28.5897869
6## x.3 13.3637110
7## x.4 27.2558797
8## x.5 .
9## x.6 26.6625588
10## x.7 30.6841774
11## x.8 -9.1388677
12## x.9 .
13## x.10 17.9220939
14## x.11 -8.2461257
15## x.12 -7.0603651
16## x.13 3.2052101
17## x.14 19.7219890
18## x.15 .
19## x.16 7.2082509
20## x.17 10.4137411
21## x.18 -0.6693664
22## x.19 21.5357460
23## x.20 20.5226071
1ggplot(lassoCol)
1lassoPred<-predict(lassoCol,test_set)
2lassoPred %>% postResample(obs = test_set$y)
1## RMSE Rsquared MAE
2## 2.7289452 0.9992454 2.2029482
1mGrid <- expand.grid(ncomp=seq(from=1,to=20,length=10))
1pcrCol<-train(y~.,data=train_set,method="pcr",tuneGrid = mGrid)
2pcrCol %>% summary %>% print
1## Data: X dimension: 100 20
2## Y dimension: 100 1
3## Fit method: svdpc
4## Number of components considered: 20
5## TRAINING: % variance explained
6## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
7## X 10.040 18.46 26.62 34.56 41.87 48.54 54.56
8## .outcome 8.425 34.90 41.09 43.12 45.06 48.09 66.44
9## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
10## X 60.33 65.37 70.01 74.46 78.72 82.32 85.67
11## .outcome 85.76 88.81 89.93 91.66 91.91 92.04 92.08
12## 15 comps 16 comps 17 comps 18 comps 19 comps 20 comps
13## X 88.85 91.94 94.59 96.73 98.51 100.00
14## .outcome 92.15 94.96 99.51 99.57 99.76 99.99
15## NULL
1ggplot(pcrCol)
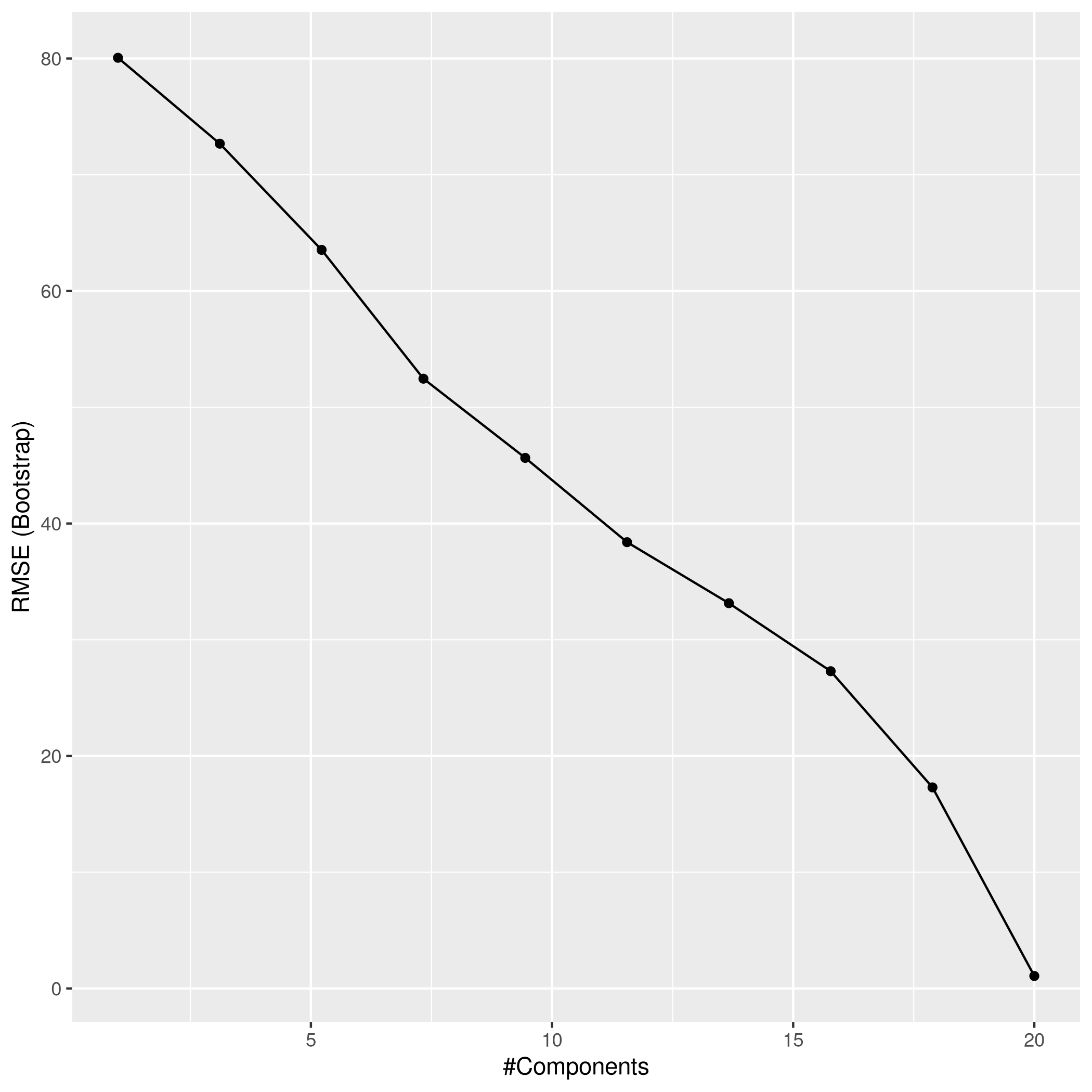
1pcrPred<-predict(pcrCol,test_set)
2pcrPred %>% postResample(obs = test_set$y)
1## RMSE Rsquared MAE
2## 1.2151815 0.9997265 0.9638378
1plsCol<-train(y~.,data=train_set,method="pls",tuneGrid = mGrid)
2plsCol %>% summary %>% print
1## Data: X dimension: 100 20
2## Y dimension: 100 1
3## Fit method: oscorespls
4## Number of components considered: 20
5## TRAINING: % variance explained
6## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
7## X 7.762 14.79 21.01 26.89 31.55 36.13 41.12
8## .outcome 92.765 98.81 99.75 99.96 99.98 99.99 99.99
9## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
10## X 46.35 51.21 56.12 60.34 65.63 71.57 76.16
11## .outcome 99.99 99.99 99.99 99.99 99.99 99.99 99.99
12## 15 comps 16 comps 17 comps 18 comps 19 comps 20 comps
13## X 80.72 84.69 88.98 92.69 96.71 100.00
14## .outcome 99.99 99.99 99.99 99.99 99.99 99.99
15## NULL
1ggplot(plsCol)
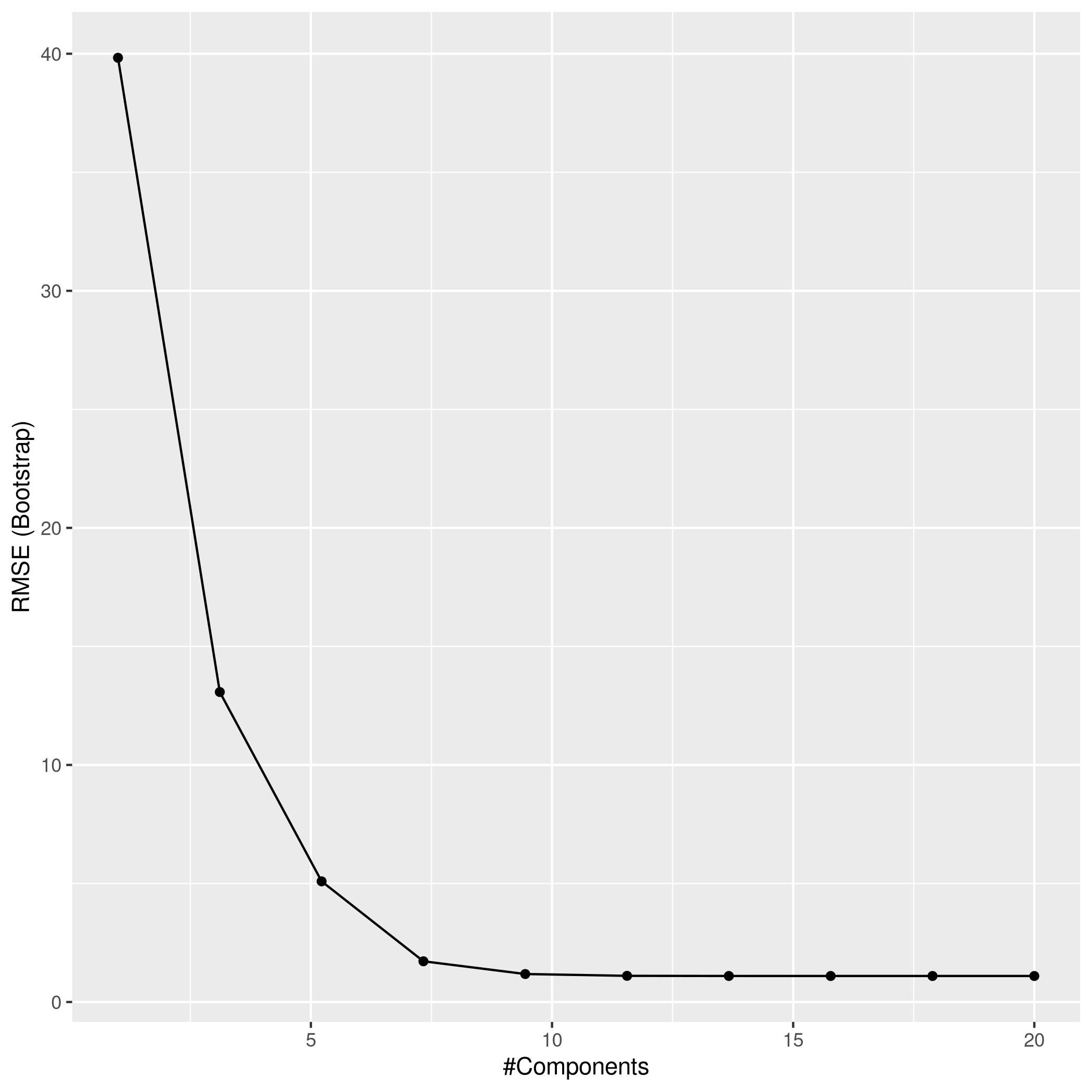
1plsPred<-predict(plsCol,test_set)
2plsPred %>% postResample(obs = test_set$y)
1## RMSE Rsquared MAE
2## 1.2151815 0.9997265 0.9638378
d) Test MSE for best models
- All the models have the same R² but Ridge does the worst followed by LASSO
For the rest of the question, we will consider the OLS model.
1modelFit<-regsubsets(y~.,data=modelDat,nvmax=20)
2modelFit %>% summary %>% print
1## Subset selection object
2## Call: regsubsets.formula(y ~ ., data = modelDat, nvmax = 20)
3## 20 Variables (and intercept)
4## Forced in Forced out
5## x.1 FALSE FALSE
6## x.2 FALSE FALSE
7## x.3 FALSE FALSE
8## x.4 FALSE FALSE
9## x.5 FALSE FALSE
10## x.6 FALSE FALSE
11## x.7 FALSE FALSE
12## x.8 FALSE FALSE
13## x.9 FALSE FALSE
14## x.10 FALSE FALSE
15## x.11 FALSE FALSE
16## x.12 FALSE FALSE
17## x.13 FALSE FALSE
18## x.14 FALSE FALSE
19## x.15 FALSE FALSE
20## x.16 FALSE FALSE
21## x.17 FALSE FALSE
22## x.18 FALSE FALSE
23## x.19 FALSE FALSE
24## x.20 FALSE FALSE
25## 1 subsets of each size up to 20
26## Selection Algorithm: exhaustive
27## x.1 x.2 x.3 x.4 x.5 x.6 x.7 x.8 x.9 x.10 x.11 x.12 x.13 x.14 x.15
28## 1 ( 1 ) " " " " " " " " " " " " "*" " " " " " " " " " " " " " " " "
29## 2 ( 1 ) " " " " " " " " " " "*" "*" " " " " " " " " " " " " " " " "
30## 3 ( 1 ) " " "*" " " " " " " "*" "*" " " " " " " " " " " " " " " " "
31## 4 ( 1 ) " " "*" " " "*" " " "*" "*" " " " " " " " " " " " " " " " "
32## 5 ( 1 ) " " "*" " " "*" " " "*" "*" " " " " " " " " " " " " "*" " "
33## 6 ( 1 ) " " "*" " " "*" " " "*" "*" " " " " " " " " " " " " " " " "
34## 7 ( 1 ) " " "*" " " "*" " " "*" "*" " " " " " " " " " " " " "*" " "
35## 8 ( 1 ) " " "*" " " "*" " " "*" "*" " " " " "*" " " " " " " "*" " "
36## 9 ( 1 ) " " "*" "*" "*" " " "*" "*" " " " " "*" " " " " " " "*" " "
37## 10 ( 1 ) " " "*" "*" "*" " " "*" "*" " " " " "*" " " " " " " "*" " "
38## 11 ( 1 ) " " "*" "*" "*" " " "*" "*" " " " " "*" "*" " " " " "*" " "
39## 12 ( 1 ) " " "*" "*" "*" " " "*" "*" "*" " " "*" "*" " " " " "*" " "
40## 13 ( 1 ) " " "*" "*" "*" " " "*" "*" "*" " " "*" "*" "*" " " "*" " "
41## 14 ( 1 ) " " "*" "*" "*" " " "*" "*" "*" " " "*" "*" "*" " " "*" " "
42## 15 ( 1 ) " " "*" "*" "*" " " "*" "*" "*" " " "*" "*" "*" "*" "*" " "
43## 16 ( 1 ) " " "*" "*" "*" " " "*" "*" "*" " " "*" "*" "*" "*" "*" " "
44## 17 ( 1 ) "*" "*" "*" "*" " " "*" "*" "*" " " "*" "*" "*" "*" "*" " "
45## 18 ( 1 ) "*" "*" "*" "*" " " "*" "*" "*" " " "*" "*" "*" "*" "*" "*"
46## 19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" "*"
47## 20 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
48## x.16 x.17 x.18 x.19 x.20
49## 1 ( 1 ) " " " " " " " " " "
50## 2 ( 1 ) " " " " " " " " " "
51## 3 ( 1 ) " " " " " " " " " "
52## 4 ( 1 ) " " " " " " " " " "
53## 5 ( 1 ) " " " " " " " " " "
54## 6 ( 1 ) " " " " " " "*" "*"
55## 7 ( 1 ) " " " " " " "*" "*"
56## 8 ( 1 ) " " " " " " "*" "*"
57## 9 ( 1 ) " " " " " " "*" "*"
58## 10 ( 1 ) " " "*" " " "*" "*"
59## 11 ( 1 ) " " "*" " " "*" "*"
60## 12 ( 1 ) " " "*" " " "*" "*"
61## 13 ( 1 ) " " "*" " " "*" "*"
62## 14 ( 1 ) "*" "*" " " "*" "*"
63## 15 ( 1 ) "*" "*" " " "*" "*"
64## 16 ( 1 ) "*" "*" "*" "*" "*"
65## 17 ( 1 ) "*" "*" "*" "*" "*"
66## 18 ( 1 ) "*" "*" "*" "*" "*"
67## 19 ( 1 ) "*" "*" "*" "*" "*"
68## 20 ( 1 ) "*" "*" "*" "*" "*"
We might want to take a look at these.
1par(mfrow=c(2,2))
2plot(modelFit)
3plot(modelFit,scale='Cp')
4plot(modelFit,scale='r2')
5plot(modelFit,scale='adjr2')
1plotLEAP(modelFit %>% summary)
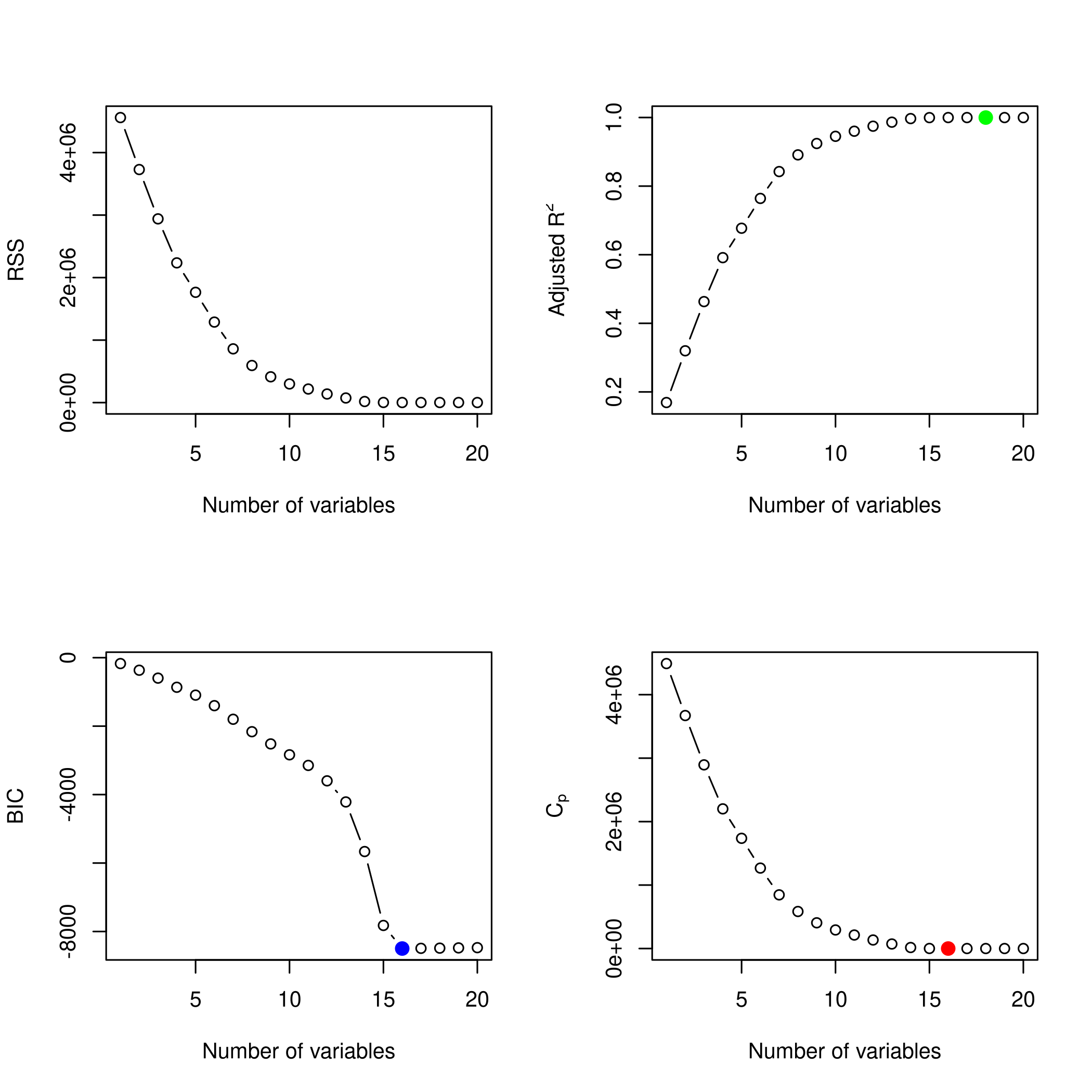
It would appear that 16 variables would be a good bet. We note that the lasso model did void out 4 parameters, namely x₁,x₃,x₁₃ and x₁₇.
Lets take a quick look at the various model variable significance values.
1lgp<-linCol %>% varImp %>% ggplot + ggtitle("OLS Variable Importance")
2rgp<-ridgCol %>% varImp %>% ggplot + ggtitle("Ridge Variable Importance")
3lsgp<-lassoCol %>% varImp %>% ggplot + ggtitle("Lasso Variable Importance")
4pcgp<-pcrCol %>% varImp %>% ggplot + ggtitle("PCR Variable Importance")
5plgp<-plsCol %>% varImp %>% ggplot + ggtitle("PLS Variable Importance")
6grid.arrange(lgp,rgp,lsgp,pcgp,plgp,ncol=3,bottom="Effective Importance, scaled")
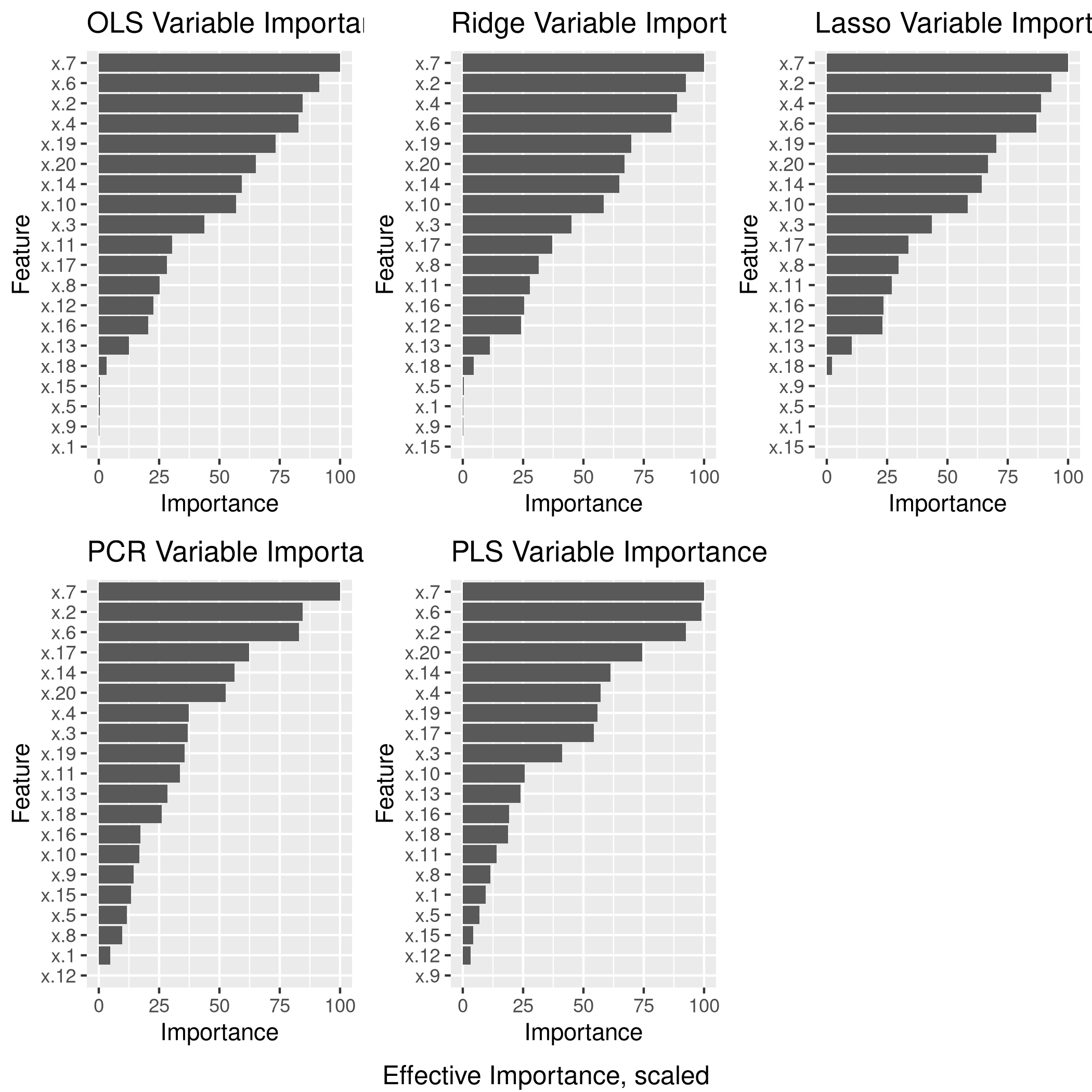
e) Model size
The test set numeric minimum RMSE is a tie between OLS and PCR, and this was achieved for the (effective) 16 variable OLS model, as well as the 18 variable PCR model.
f) Best model
We will consider the OLS and PCR models and its parameters.
1linCol$finalModel %>% print
1##
2## Call:
3## lm(formula = .outcome ~ ., data = dat)
4##
5## Coefficients:
6## (Intercept) x.1 x.2 x.3 x.4 x.5
7## -0.06052 -0.02265 28.91650 14.16532 28.16256 0.13742
8## x.6 x.7 x.8 x.9 x.10 x.11
9## 27.01497 31.15917 -9.66308 0.11641 19.06687 -9.09956
10## x.12 x.13 x.14 x.15 x.16 x.17
11## -8.01933 4.26852 20.22366 -0.16607 7.95594 10.89851
12## x.18 x.19 x.20
13## -1.09760 22.05197 20.88796
1pcrCol$bestTune %>% print
1## ncomp
2## 10 20
Now to compare this to the original.
1beta %>% print
1## [1] 0 29 14 28 0 27 31 -10 0 19 -9 -8 4 20 0 8 11 -1 22
2## [20] 21
1t=data.frame(linCol$finalModel$coefficients[-1]) %>% rename("Model_Coeffs"=1) %>% add_column(beta) %>% rename("Original_Coeffs"=2)
2print(t)
1## Model_Coeffs Original_Coeffs
2## x.1 -0.02265289 0
3## x.2 28.91649699 29
4## x.3 14.16532050 14
5## x.4 28.16255937 28
6## x.5 0.13741621 0
7## x.6 27.01497459 27
8## x.7 31.15917172 31
9## x.8 -9.66308362 -10
10## x.9 0.11641282 0
11## x.10 19.06687041 19
12## x.11 -9.09955826 -9
13## x.12 -8.01932598 -8
14## x.13 4.26852334 4
15## x.14 20.22366153 20
16## x.15 -0.16606531 0
17## x.16 7.95593559 8
18## x.17 10.89851353 11
19## x.18 -1.09759687 -1
20## x.19 22.05196537 22
21## x.20 20.88795623 21
We see that the coefficients are pretty similar.
g) Plotting differences
1val.errors = rep(NaN, p)
2a = rep(NaN, p)
3b = rep(NaN, p)
4x_cols = colnames(xmat, do.NULL = FALSE, prefix = "x.")
5for (i in 1:p) {
6 coefi = coef(modelFit, id = i)
7 a[i] = length(coefi) - 1 ## Not counting the intercept
8 b[i] = sqrt(sum((beta[x_cols %in% names(coefi)] - coefi[names(coefi) %in% x_cols])^2) +
9 sum(beta[!(x_cols %in% names(coefi))])^2) ## Handling the intercept
10}
11plot(x = a, y = b, xlab = "Number of Coefficients", ylab = "Relative Error")
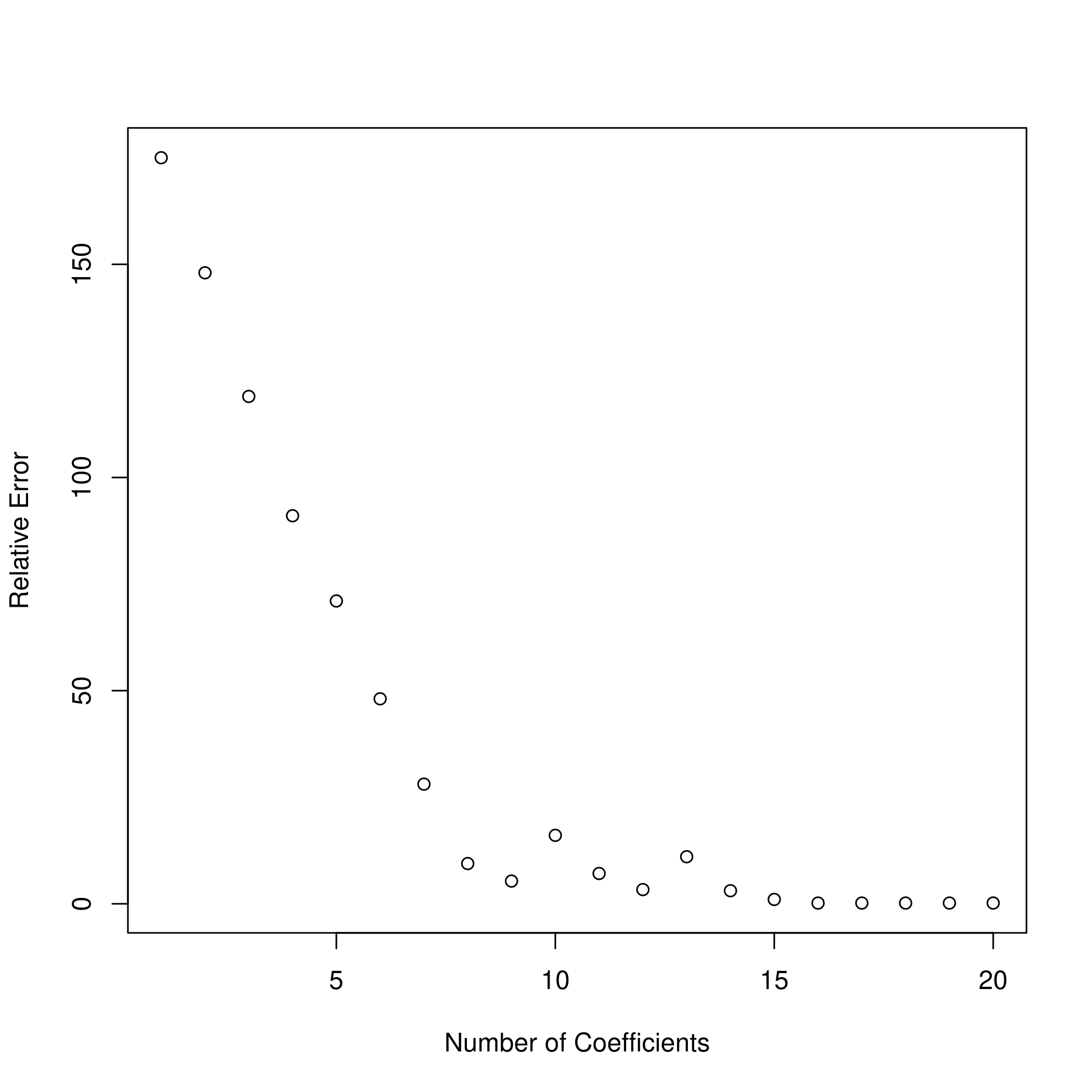
Question 6.11 - Page 264
We will now try to predict per capita crime rate in the Boston data set.
(a) Try out some of the regression methods explored in this chapter, such as best subset selection, the lasso, ridge regression, and PCR. Present and discuss results for the approaches that you consider.
(b) Propose a model (or set of models) that seem to perform well on this data set, and justify your answer. Make sure that you are evaluating model performance using validation set error, crossvalidation, or some other reasonable alternative, as opposed to using training error.
(c) Does your chosen model involve all of the features in the data set? Why or why not?
Answer
1boston<-MASS::Boston
- Summarize
1boston %>% str %>% print
1## 'data.frame': 506 obs. of 14 variables:
2## $ crim : num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
3## $ zn : num 18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
4## $ indus : num 2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
5## $ chas : int 0 0 0 0 0 0 0 0 0 0 ...
6## $ nox : num 0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
7## $ rm : num 6.58 6.42 7.18 7 7.15 ...
8## $ age : num 65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
9## $ dis : num 4.09 4.97 4.97 6.06 6.06 ...
10## $ rad : int 1 2 2 3 3 3 5 5 5 5 ...
11## $ tax : num 296 242 242 222 222 222 311 311 311 311 ...
12## $ ptratio: num 15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
13## $ black : num 397 397 393 395 397 ...
14## $ lstat : num 4.98 9.14 4.03 2.94 5.33 ...
15## $ medv : num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...
16## NULL
1boston %>% summary %>% print
1## crim zn indus chas
2## Min. : 0.00632 Min. : 0.00 Min. : 0.46 Min. :0.00000
3## 1st Qu.: 0.08204 1st Qu.: 0.00 1st Qu.: 5.19 1st Qu.:0.00000
4## Median : 0.25651 Median : 0.00 Median : 9.69 Median :0.00000
5## Mean : 3.61352 Mean : 11.36 Mean :11.14 Mean :0.06917
6## 3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10 3rd Qu.:0.00000
7## Max. :88.97620 Max. :100.00 Max. :27.74 Max. :1.00000
8## nox rm age dis
9## Min. :0.3850 Min. :3.561 Min. : 2.90 Min. : 1.130
10## 1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 45.02 1st Qu.: 2.100
11## Median :0.5380 Median :6.208 Median : 77.50 Median : 3.207
12## Mean :0.5547 Mean :6.285 Mean : 68.57 Mean : 3.795
13## 3rd Qu.:0.6240 3rd Qu.:6.623 3rd Qu.: 94.08 3rd Qu.: 5.188
14## Max. :0.8710 Max. :8.780 Max. :100.00 Max. :12.127
15## rad tax ptratio black
16## Min. : 1.000 Min. :187.0 Min. :12.60 Min. : 0.32
17## 1st Qu.: 4.000 1st Qu.:279.0 1st Qu.:17.40 1st Qu.:375.38
18## Median : 5.000 Median :330.0 Median :19.05 Median :391.44
19## Mean : 9.549 Mean :408.2 Mean :18.46 Mean :356.67
20## 3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.23
21## Max. :24.000 Max. :711.0 Max. :22.00 Max. :396.90
22## lstat medv
23## Min. : 1.73 Min. : 5.00
24## 1st Qu.: 6.95 1st Qu.:17.02
25## Median :11.36 Median :21.20
26## Mean :12.65 Mean :22.53
27## 3rd Qu.:16.95 3rd Qu.:25.00
28## Max. :37.97 Max. :50.00
1boston %>% sapply(unique) %>% sapply(length) %>% print
1## crim zn indus chas nox rm age dis rad tax
2## 504 26 76 2 81 446 356 412 9 66
3## ptratio black lstat medv
4## 46 357 455 229
a) Test regression models
1train_ind = sample(boston %>% nrow,100)
2test_ind = setdiff(seq_len(boston %>% nrow), train_set)
1train_set<-boston[train_ind,]
2test_set<-boston[-train_ind,]
1linCol<-train(crim~.,data=train_set,method="lm")
2linCol %>% summary
1##
2## Call:
3## lm(formula = .outcome ~ ., data = dat)
4##
5## Residuals:
6## Min 1Q Median 3Q Max
7## -6.2431 -1.0344 -0.0563 0.8187 8.1318
8##
9## Coefficients:
10## Estimate Std. Error t value Pr(>|t|)
11## (Intercept) 0.9339246 7.6508393 0.122 0.9031
12## zn 0.0046819 0.0157375 0.297 0.7668
13## indus 0.0276209 0.0875254 0.316 0.7531
14## chas -1.1602278 1.2386869 -0.937 0.3516
15## nox -7.5024503 5.0207818 -1.494 0.1388
16## rm 1.1240874 0.7462340 1.506 0.1356
17## age 0.0020182 0.0137404 0.147 0.8836
18## dis -0.3934753 0.2454365 -1.603 0.1126
19## rad 0.4540613 0.0791580 5.736 1.41e-07 ***
20## tax 0.0008469 0.0052593 0.161 0.8724
21## ptratio -0.2978204 0.1637629 -1.819 0.0725 .
22## black 0.0030642 0.0045281 0.677 0.5004
23## lstat 0.1322779 0.0626485 2.111 0.0376 *
24## medv -0.0841382 0.0590700 -1.424 0.1580
25## ---
26## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
27##
28## Residual standard error: 2.362 on 86 degrees of freedom
29## Multiple R-squared: 0.775, Adjusted R-squared: 0.741
30## F-statistic: 22.78 on 13 and 86 DF, p-value: < 2.2e-16
1linPred<-predict(linCol,test_set)
2linPred %>% postResample(obs = test_set$crim)
1## RMSE Rsquared MAE
2## 7.3794735 0.4056002 2.6774969
1L2Grid <- expand.grid(alpha=0,
2 lambda=10^seq(from=-3,to=30,length=100))
1ridgCol<-train(crim~.,data=train_set,method="glmnet",tuneGrid = L2Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1ridgCol %>% summary %>% print
1## Length Class Mode
2## a0 100 -none- numeric
3## beta 1300 dgCMatrix S4
4## df 100 -none- numeric
5## dim 2 -none- numeric
6## lambda 100 -none- numeric
7## dev.ratio 100 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 13 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(ridgCol$finalModel, ridgCol$bestTune$lambda) %>% print
1## 14 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) -3.881166065
4## zn 0.002597790
5## indus -0.005103517
6## chas -0.674764337
7## nox -0.053645732
8## rm 0.600064844
9## age 0.001153570
10## dis -0.179295384
11## rad 0.267082956
12## tax 0.006447932
13## ptratio -0.075885753
14## black -0.001650403
15## lstat 0.086462700
16## medv -0.027519270
1ggplot(ridgCol)
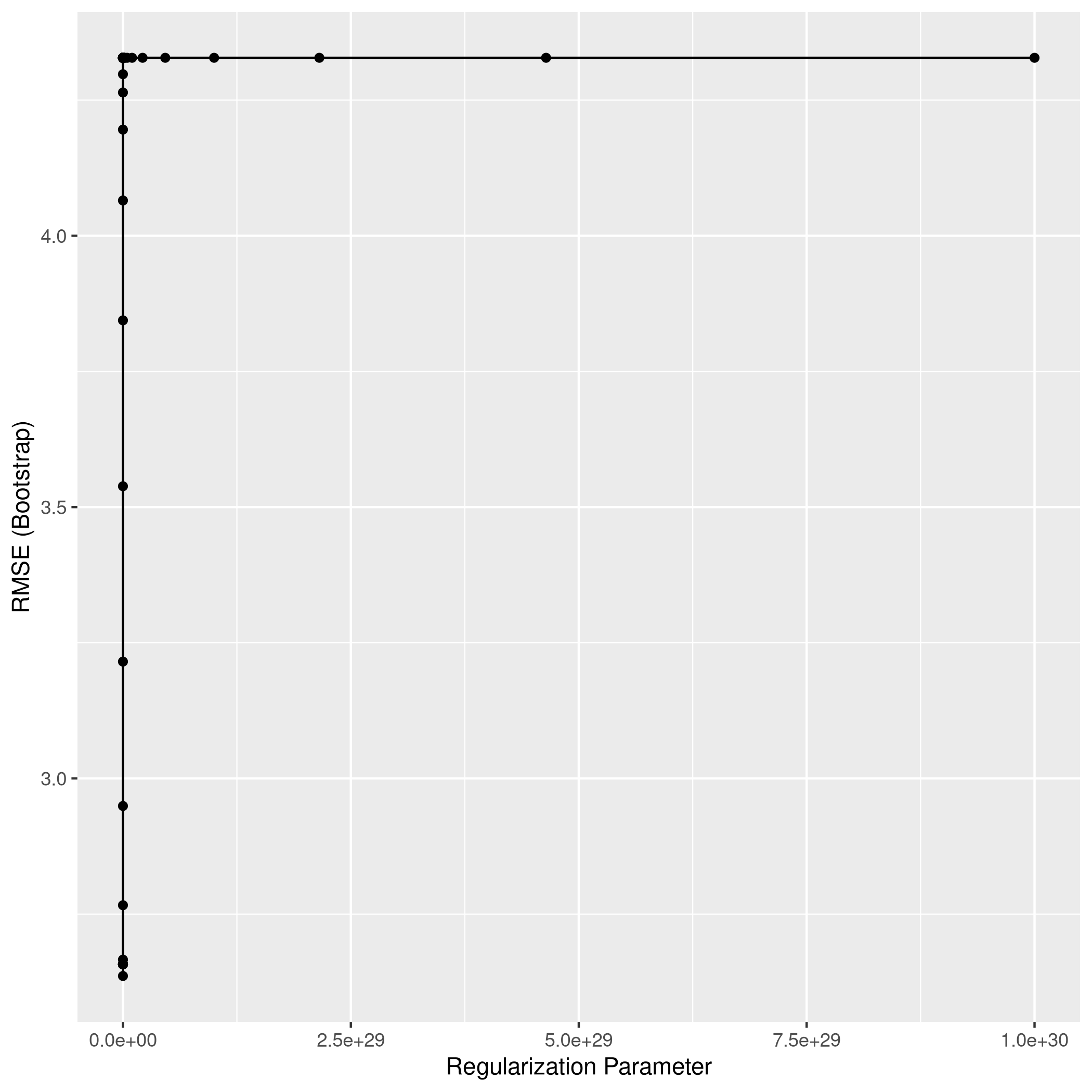
1ridgPred<-predict(ridgCol,test_set)
2ridgPred %>% postResample(obs = test_set$crim)
1## RMSE Rsquared MAE
2## 7.5065916 0.4017056 2.4777547
1L1Grid <- expand.grid(alpha=1, # for lasso
2 lambda=10^seq(from=-3,to=30,length=100))
1lassoCol<-train(crim~.,data=train_set,method="glmnet",tuneGrid = L1Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1lassoCol %>% summary %>% print
1## Length Class Mode
2## a0 78 -none- numeric
3## beta 1014 dgCMatrix S4
4## df 78 -none- numeric
5## dim 2 -none- numeric
6## lambda 78 -none- numeric
7## dev.ratio 78 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 13 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(lassoCol$finalModel, lassoCol$bestTune$lambda) %>% print
1## 14 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) -2.024006430
4## zn .
5## indus .
6## chas .
7## nox .
8## rm .
9## age .
10## dis -0.008506188
11## rad 0.386379255
12## tax 0.001779579
13## ptratio .
14## black .
15## lstat 0.040788606
16## medv .
1ggplot(lassoCol)
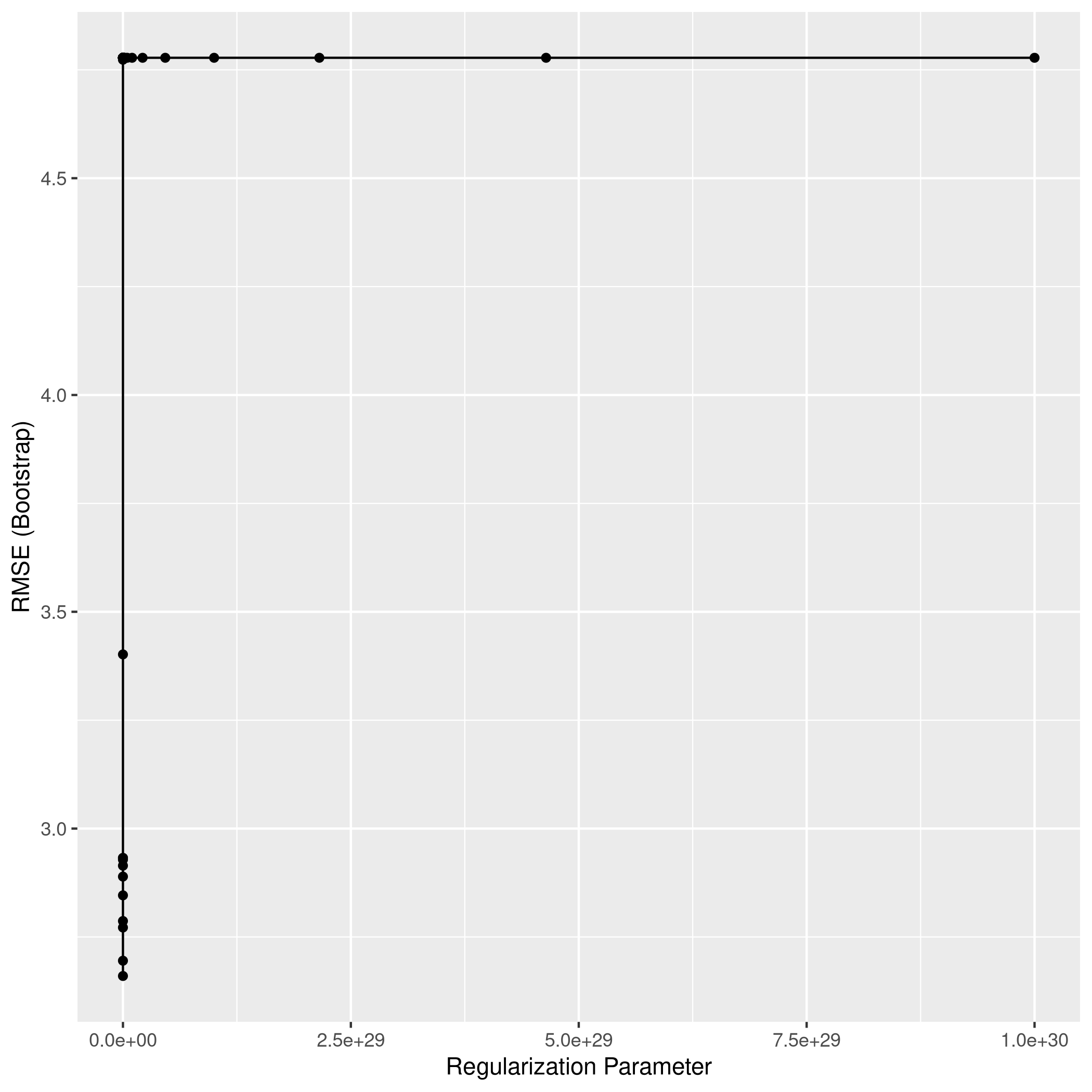
1lassoPred<-predict(lassoCol,test_set)
2lassoPred %>% postResample(obs = test_set$crim)
1## RMSE Rsquared MAE
2## 7.5868293 0.3859121 2.4892258
1mGrid <- expand.grid(ncomp=seq(from=1,to=20,length=10))
- All the models have the same R² but Ridge does the worst followed by LASSO
For the rest of the question, we will consider the OLS model.
1modelFit<-regsubsets(crim~.,data=boston,nvmax=20)
2modelFit %>% summary %>% print
1## Subset selection object
2## Call: regsubsets.formula(crim ~ ., data = boston, nvmax = 20)
3## 13 Variables (and intercept)
4## Forced in Forced out
5## zn FALSE FALSE
6## indus FALSE FALSE
7## chas FALSE FALSE
8## nox FALSE FALSE
9## rm FALSE FALSE
10## age FALSE FALSE
11## dis FALSE FALSE
12## rad FALSE FALSE
13## tax FALSE FALSE
14## ptratio FALSE FALSE
15## black FALSE FALSE
16## lstat FALSE FALSE
17## medv FALSE FALSE
18## 1 subsets of each size up to 13
19## Selection Algorithm: exhaustive
20## zn indus chas nox rm age dis rad tax ptratio black lstat medv
21## 1 ( 1 ) " " " " " " " " " " " " " " "*" " " " " " " " " " "
22## 2 ( 1 ) " " " " " " " " " " " " " " "*" " " " " " " "*" " "
23## 3 ( 1 ) " " " " " " " " " " " " " " "*" " " " " "*" "*" " "
24## 4 ( 1 ) "*" " " " " " " " " " " "*" "*" " " " " " " " " "*"
25## 5 ( 1 ) "*" " " " " " " " " " " "*" "*" " " " " "*" " " "*"
26## 6 ( 1 ) "*" " " " " "*" " " " " "*" "*" " " " " "*" " " "*"
27## 7 ( 1 ) "*" " " " " "*" " " " " "*" "*" " " "*" "*" " " "*"
28## 8 ( 1 ) "*" " " " " "*" " " " " "*" "*" " " "*" "*" "*" "*"
29## 9 ( 1 ) "*" "*" " " "*" " " " " "*" "*" " " "*" "*" "*" "*"
30## 10 ( 1 ) "*" "*" " " "*" "*" " " "*" "*" " " "*" "*" "*" "*"
31## 11 ( 1 ) "*" "*" " " "*" "*" " " "*" "*" "*" "*" "*" "*" "*"
32## 12 ( 1 ) "*" "*" "*" "*" "*" " " "*" "*" "*" "*" "*" "*" "*"
33## 13 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
We might want to take a look at these.
1par(mfrow=c(2,2))
2plot(modelFit)
3plot(modelFit,scale='Cp')
4plot(modelFit,scale='r2')
5plot(modelFit,scale='adjr2')
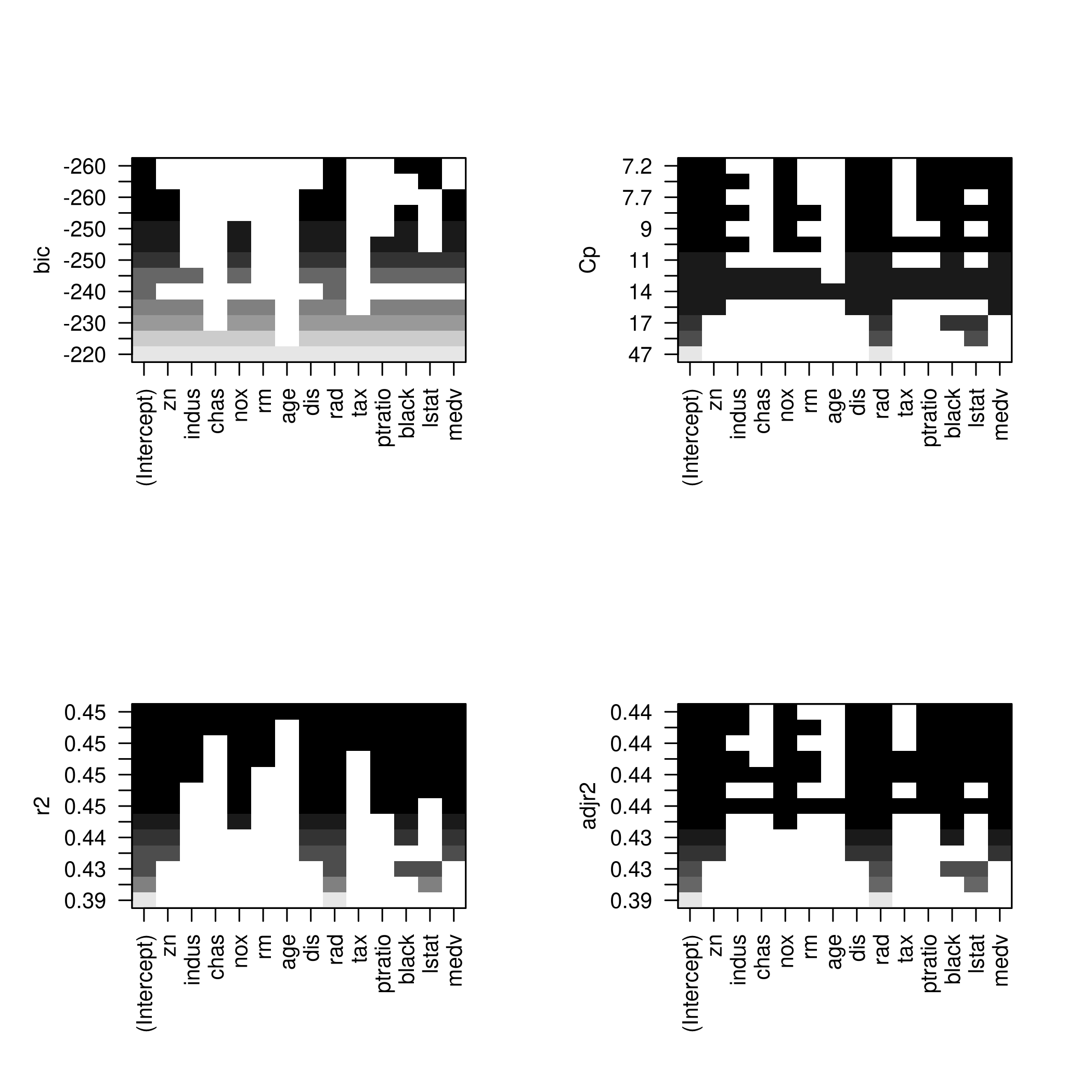
1plotLEAP(modelFit %>% summary)
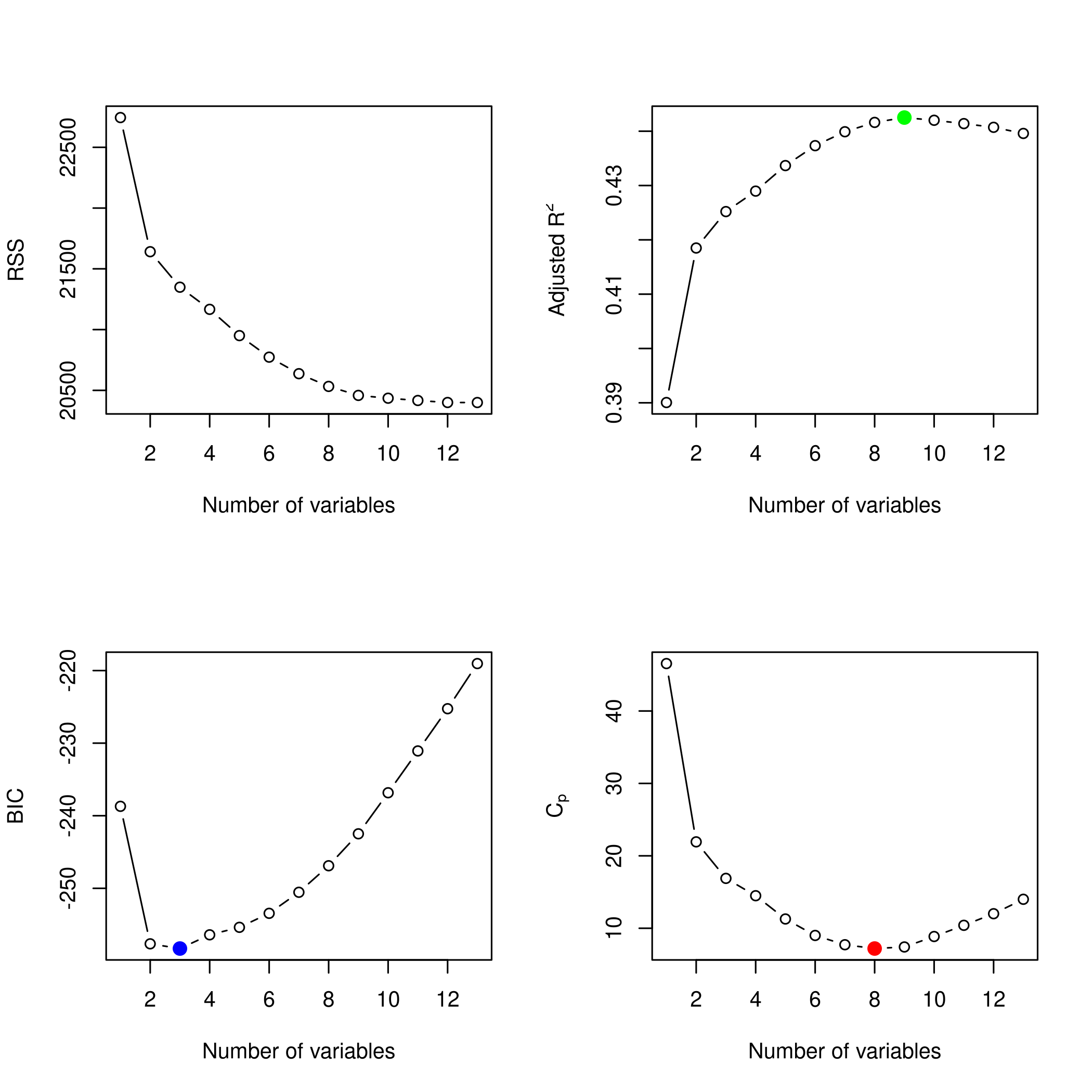
It would appear that 16 variables would be a good bet. We note that the lasso model did void out 4 parameters, namely x₁,x₃,x₁₃ and x₁₇.
Lets take a quick look at the various model variable significance values.
1lgp<-linCol %>% varImp %>% ggplot + ggtitle("OLS Variable Importance")
2rgp<-ridgCol %>% varImp %>% ggplot + ggtitle("Ridge Variable Importance")
3lsgp<-lassoCol %>% varImp %>% ggplot + ggtitle("Lasso Variable Importance")
4grid.arrange(lgp,rgp,lsgp,ncol=2,bottom="Effective Importance, scaled")
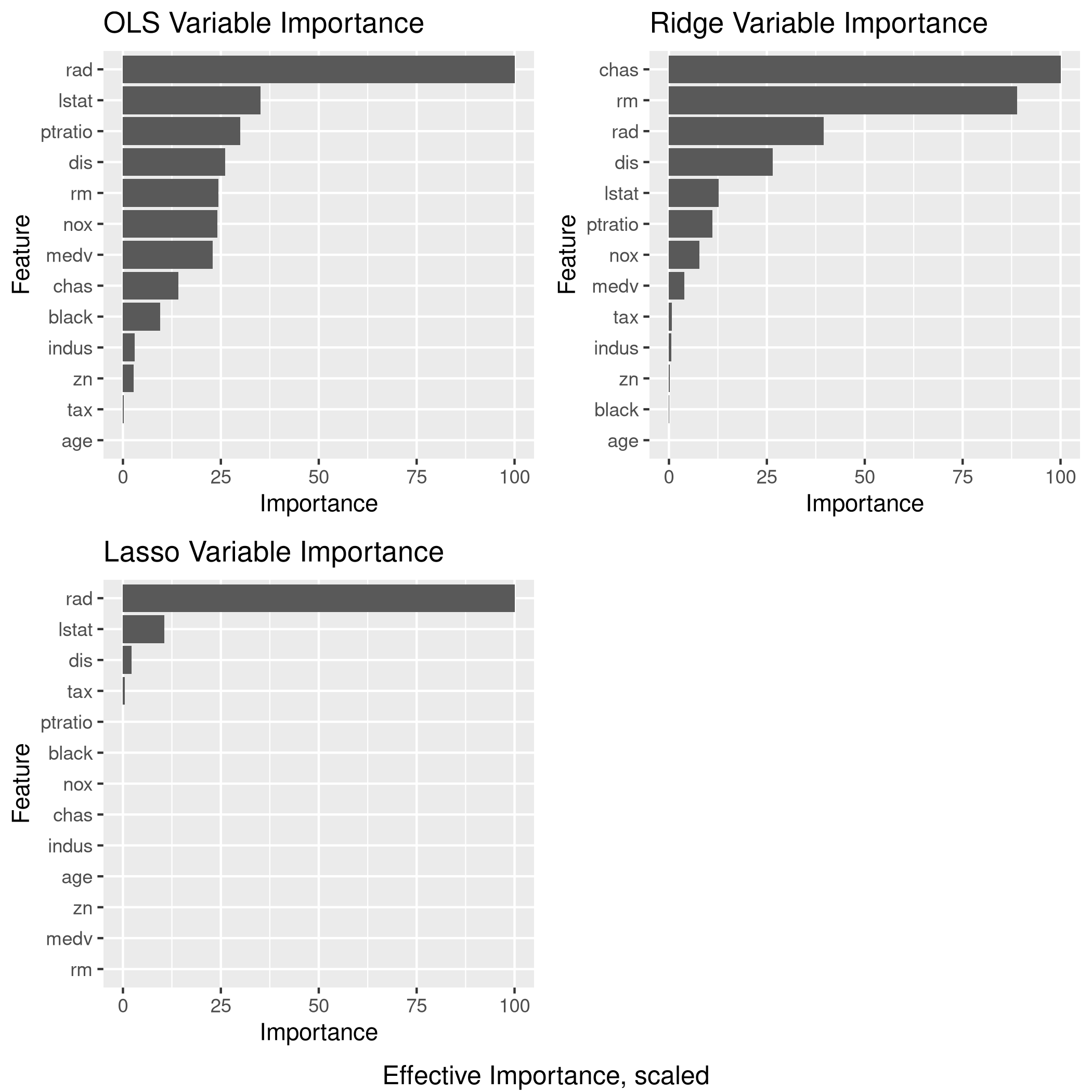
b) Propose a model
Given the data and plots, I would probably end up using the Ridge regression model
Clearly, LASSO is not working very well since it seems to have taken mainly 3 variables, one of which is largely categorical (9 levels)
c) Model properties
1boston %>% str %>% print
1## 'data.frame': 506 obs. of 14 variables:
2## $ crim : num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
3## $ zn : num 18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
4## $ indus : num 2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
5## $ chas : int 0 0 0 0 0 0 0 0 0 0 ...
6## $ nox : num 0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
7## $ rm : num 6.58 6.42 7.18 7 7.15 ...
8## $ age : num 65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
9## $ dis : num 4.09 4.97 4.97 6.06 6.06 ...
10## $ rad : int 1 2 2 3 3 3 5 5 5 5 ...
11## $ tax : num 296 242 242 222 222 222 311 311 311 311 ...
12## $ ptratio: num 15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
13## $ black : num 397 397 393 395 397 ...
14## $ lstat : num 4.98 9.14 4.03 2.94 5.33 ...
15## $ medv : num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...
16## NULL
1boston %>% summary %>% print
1## crim zn indus chas
2## Min. : 0.00632 Min. : 0.00 Min. : 0.46 Min. :0.00000
3## 1st Qu.: 0.08204 1st Qu.: 0.00 1st Qu.: 5.19 1st Qu.:0.00000
4## Median : 0.25651 Median : 0.00 Median : 9.69 Median :0.00000
5## Mean : 3.61352 Mean : 11.36 Mean :11.14 Mean :0.06917
6## 3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10 3rd Qu.:0.00000
7## Max. :88.97620 Max. :100.00 Max. :27.74 Max. :1.00000
8## nox rm age dis
9## Min. :0.3850 Min. :3.561 Min. : 2.90 Min. : 1.130
10## 1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 45.02 1st Qu.: 2.100
11## Median :0.5380 Median :6.208 Median : 77.50 Median : 3.207
12## Mean :0.5547 Mean :6.285 Mean : 68.57 Mean : 3.795
13## 3rd Qu.:0.6240 3rd Qu.:6.623 3rd Qu.: 94.08 3rd Qu.: 5.188
14## Max. :0.8710 Max. :8.780 Max. :100.00 Max. :12.127
15## rad tax ptratio black
16## Min. : 1.000 Min. :187.0 Min. :12.60 Min. : 0.32
17## 1st Qu.: 4.000 1st Qu.:279.0 1st Qu.:17.40 1st Qu.:375.38
18## Median : 5.000 Median :330.0 Median :19.05 Median :391.44
19## Mean : 9.549 Mean :408.2 Mean :18.46 Mean :356.67
20## 3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.23
21## Max. :24.000 Max. :711.0 Max. :22.00 Max. :396.90
22## lstat medv
23## Min. : 1.73 Min. : 5.00
24## 1st Qu.: 6.95 1st Qu.:17.02
25## Median :11.36 Median :21.20
26## Mean :12.65 Mean :22.53
27## 3rd Qu.:16.95 3rd Qu.:25.00
28## Max. :37.97 Max. :50.00
1boston %>% sapply(unique) %>% sapply(length) %>% print
1## crim zn indus chas nox rm age dis rad tax
2## 504 26 76 2 81 446 356 412 9 66
3## ptratio black lstat medv
4## 46 357 455 229
- A good idea would be removing
radandchasfrom the regression
1boston<-boston %>% subset(select=-c(rad,chas))
1train_ind = sample(boston %>% nrow,100)
2test_ind = setdiff(seq_len(boston %>% nrow), train_set)
1train_set<-boston[train_ind,]
2test_set<-boston[-train_ind,]
1L2Grid <- expand.grid(alpha=0,
2 lambda=10^seq(from=-3,to=30,length=100))
1ridgCol<-train(crim~.,data=train_set,method="glmnet",tuneGrid = L2Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1ridgCol %>% summary %>% print
1## Length Class Mode
2## a0 100 -none- numeric
3## beta 1100 dgCMatrix S4
4## df 100 -none- numeric
5## dim 2 -none- numeric
6## lambda 100 -none- numeric
7## dev.ratio 100 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 11 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(ridgCol$finalModel, ridgCol$bestTune$lambda) %>% print
1## 12 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) 0.23015398
4## zn 0.01595378
5## indus -0.01006683
6## nox 3.42104450
7## rm -0.05904911
8## age 0.01419585
9## dis -0.16724715
10## tax 0.01021790
11## ptratio 0.05741508
12## black -0.01414707
13## lstat 0.15519923
14## medv -0.04483670
1ggplot(ridgCol)
1ridgPred<-predict(ridgCol,test_set)
2ridgPred %>% postResample(obs = test_set$crim)
1## RMSE Rsquared MAE
2## 6.9365371 0.3619974 2.8570012
1L1Grid <- expand.grid(alpha=1, # for lasso
2 lambda=10^seq(from=-3,to=30,length=100))
1lassoCol<-train(crim~.,data=train_set,method="glmnet",tuneGrid = L1Grid)
1## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
2## There were missing values in resampled performance measures.
1lassoCol %>% summary %>% print
1## Length Class Mode
2## a0 74 -none- numeric
3## beta 814 dgCMatrix S4
4## df 74 -none- numeric
5## dim 2 -none- numeric
6## lambda 74 -none- numeric
7## dev.ratio 74 -none- numeric
8## nulldev 1 -none- numeric
9## npasses 1 -none- numeric
10## jerr 1 -none- numeric
11## offset 1 -none- logical
12## call 5 -none- call
13## nobs 1 -none- numeric
14## lambdaOpt 1 -none- numeric
15## xNames 11 -none- character
16## problemType 1 -none- character
17## tuneValue 2 data.frame list
18## obsLevels 1 -none- logical
19## param 0 -none- list
1coef(lassoCol$finalModel, lassoCol$bestTune$lambda) %>% print
1## 12 x 1 sparse Matrix of class "dgCMatrix"
2## 1
3## (Intercept) 0.86635621
4## zn .
5## indus .
6## nox .
7## rm .
8## age .
9## dis .
10## tax 0.01402174
11## ptratio .
12## black -0.01454496
13## lstat 0.15290845
14## medv .
1ggplot(lassoCol)
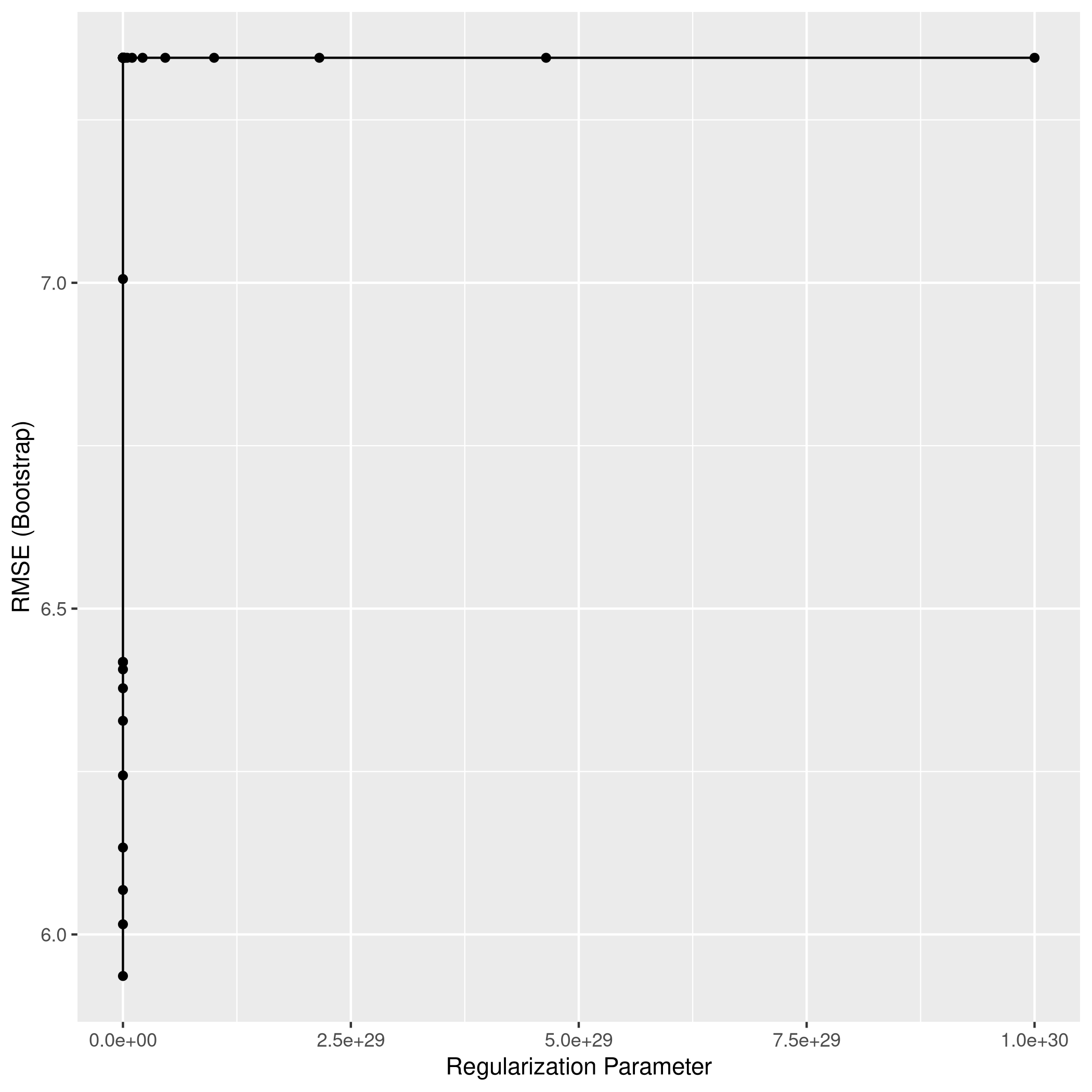
1lassoPred<-predict(lassoCol,test_set)
2lassoPred %>% postResample(obs = test_set$crim)
1## RMSE Rsquared MAE
2## 6.9630616 0.3693364 2.6767742
1rgp<-ridgCol %>% varImp %>% ggplot + ggtitle("Ridge Variable Importance")
2lsgp<-lassoCol %>% varImp %>% ggplot + ggtitle("Lasso Variable Importance")
3grid.arrange(rgp,lsgp,ncol=2,bottom="Effective Importance, scaled")
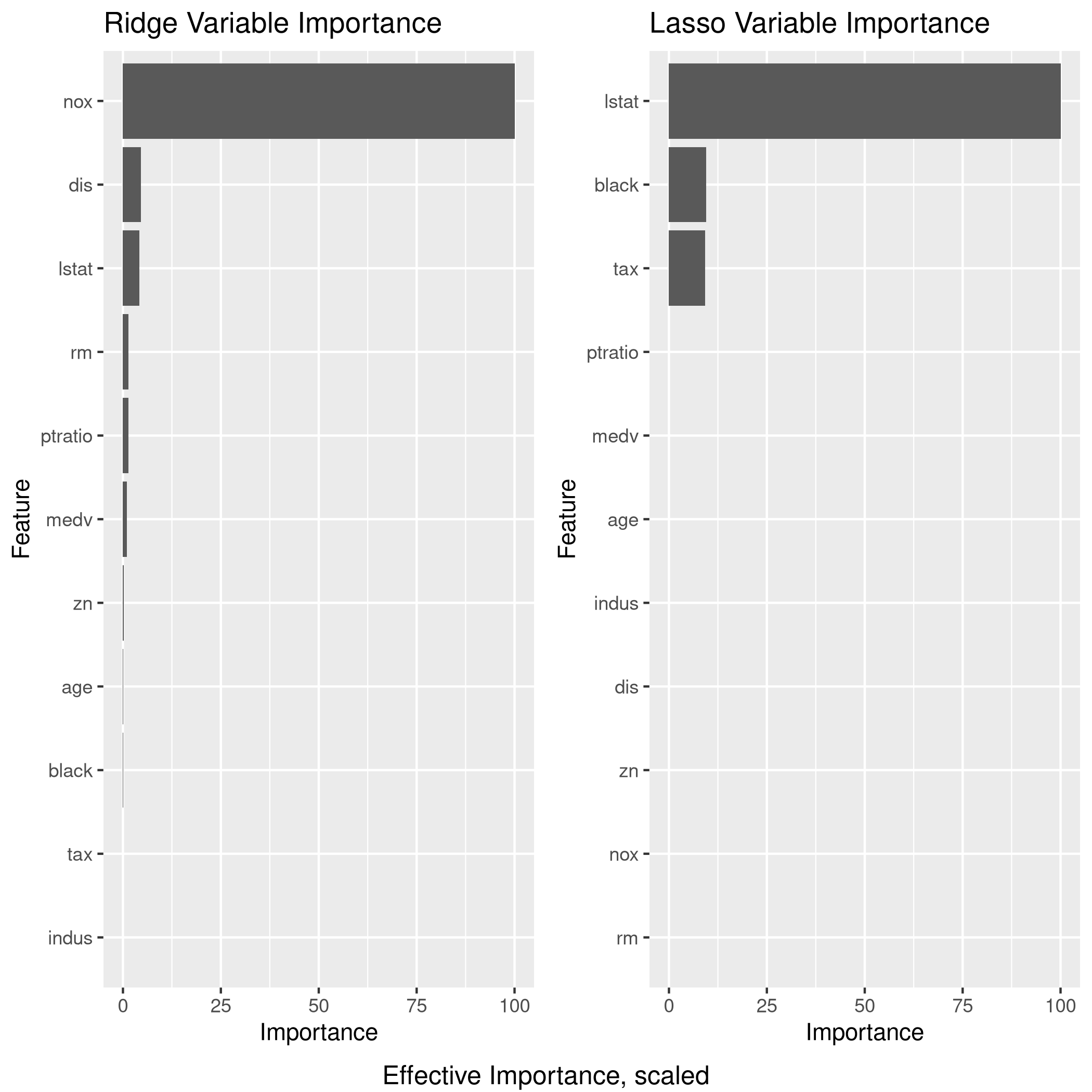
None of these models are actually any good apparently, given that we have an R² of 0.3619974 for the L2 regularization and 0.3693364 for the L1.
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: with Applications in R. Berlin, Germany: Springer Science & Business Media. ↩︎
Lang et al., (2019). mlr3: A modern object-oriented machine learning framework in R. Journal of Open Source Software, 4(44), 1903, https://doi.org/10.21105/joss.01903 ↩︎

