28 minutes
Written: 2020-02-19 09:47 +0000
ISLR :: Moving Beyond Linearity
Chapter VII - Moving Beyond Linearity
All the questions are as per the ISL seventh printing of the First edition1.
Common
1libsUsed<-c("dplyr","ggplot2","tidyverse",
2 "ISLR","caret","MASS", "gridExtra",
3 "pls","latex2exp","data.table")
4invisible(lapply(libsUsed, library, character.only = TRUE))
Question 7.6 - Page 299
In this exercise, you will further analyze the Wage data set
considered throughout this chapter.
(a) Perform polynomial regression to predict wage using age. Use
cross-validation to select the optimal degree d for the polynomial.
What degree was chosen, and how does this compare to the results of
hypothesis testing using ANOVA? Make a plot of the resulting polynomial
fit to the data.
(b) Fit a step function to predict wage using age, and perform
cross-validation to choose the optimal number of cuts. Make a plot of
the fit obtained. In this exercise, we will generate simulated data, and
will then use this data to perform best subset selection.
Answer
Lets get the data.
1set.seed(1984)
2wageDat<-ISLR::Wage
3wageDat %>% str %>% print
1## 'data.frame': 3000 obs. of 11 variables:
2## $ year : int 2006 2004 2003 2003 2005 2008 2009 2008 2006 2004 ...
3## $ age : int 18 24 45 43 50 54 44 30 41 52 ...
4## $ maritl : Factor w/ 5 levels "1. Never Married",..: 1 1 2 2 4 2 2 1 1 2 ...
5## $ race : Factor w/ 4 levels "1. White","2. Black",..: 1 1 1 3 1 1 4 3 2 1 ...
6## $ education : Factor w/ 5 levels "1. < HS Grad",..: 1 4 3 4 2 4 3 3 3 2 ...
7## $ region : Factor w/ 9 levels "1. New England",..: 2 2 2 2 2 2 2 2 2 2 ...
8## $ jobclass : Factor w/ 2 levels "1. Industrial",..: 1 2 1 2 2 2 1 2 2 2 ...
9## $ health : Factor w/ 2 levels "1. <=Good","2. >=Very Good": 1 2 1 2 1 2 2 1 2 2 ...
10## $ health_ins: Factor w/ 2 levels "1. Yes","2. No": 2 2 1 1 1 1 1 1 1 1 ...
11## $ logwage : num 4.32 4.26 4.88 5.04 4.32 ...
12## $ wage : num 75 70.5 131 154.7 75 ...
13## NULL
1wageDat %>% summary %>% print
1## year age maritl race
2## Min. :2003 Min. :18.00 1. Never Married: 648 1. White:2480
3## 1st Qu.:2004 1st Qu.:33.75 2. Married :2074 2. Black: 293
4## Median :2006 Median :42.00 3. Widowed : 19 3. Asian: 190
5## Mean :2006 Mean :42.41 4. Divorced : 204 4. Other: 37
6## 3rd Qu.:2008 3rd Qu.:51.00 5. Separated : 55
7## Max. :2009 Max. :80.00
8##
9## education region jobclass
10## 1. < HS Grad :268 2. Middle Atlantic :3000 1. Industrial :1544
11## 2. HS Grad :971 1. New England : 0 2. Information:1456
12## 3. Some College :650 3. East North Central: 0
13## 4. College Grad :685 4. West North Central: 0
14## 5. Advanced Degree:426 5. South Atlantic : 0
15## 6. East South Central: 0
16## (Other) : 0
17## health health_ins logwage wage
18## 1. <=Good : 858 1. Yes:2083 Min. :3.000 Min. : 20.09
19## 2. >=Very Good:2142 2. No : 917 1st Qu.:4.447 1st Qu.: 85.38
20## Median :4.653 Median :104.92
21## Mean :4.654 Mean :111.70
22## 3rd Qu.:4.857 3rd Qu.:128.68
23## Max. :5.763 Max. :318.34
24##
1wageDat %>% sapply(unique) %>% sapply(length) %>% print
1## year age maritl race education region jobclass
2## 7 61 5 4 5 1 2
3## health health_ins logwage wage
4## 2 2 508 508
1library(boot)
1##
2## Attaching package: 'boot'
1## The following object is masked from 'package:lattice':
2##
3## melanoma
a) Polynomial regression
1all.deltas = rep(NA, 10)
2for (i in 1:10) {
3 glm.fit = glm(wage~poly(age, i), data=Wage)
4 all.deltas[i] = cv.glm(Wage, glm.fit, K=10)$delta[2]
5}
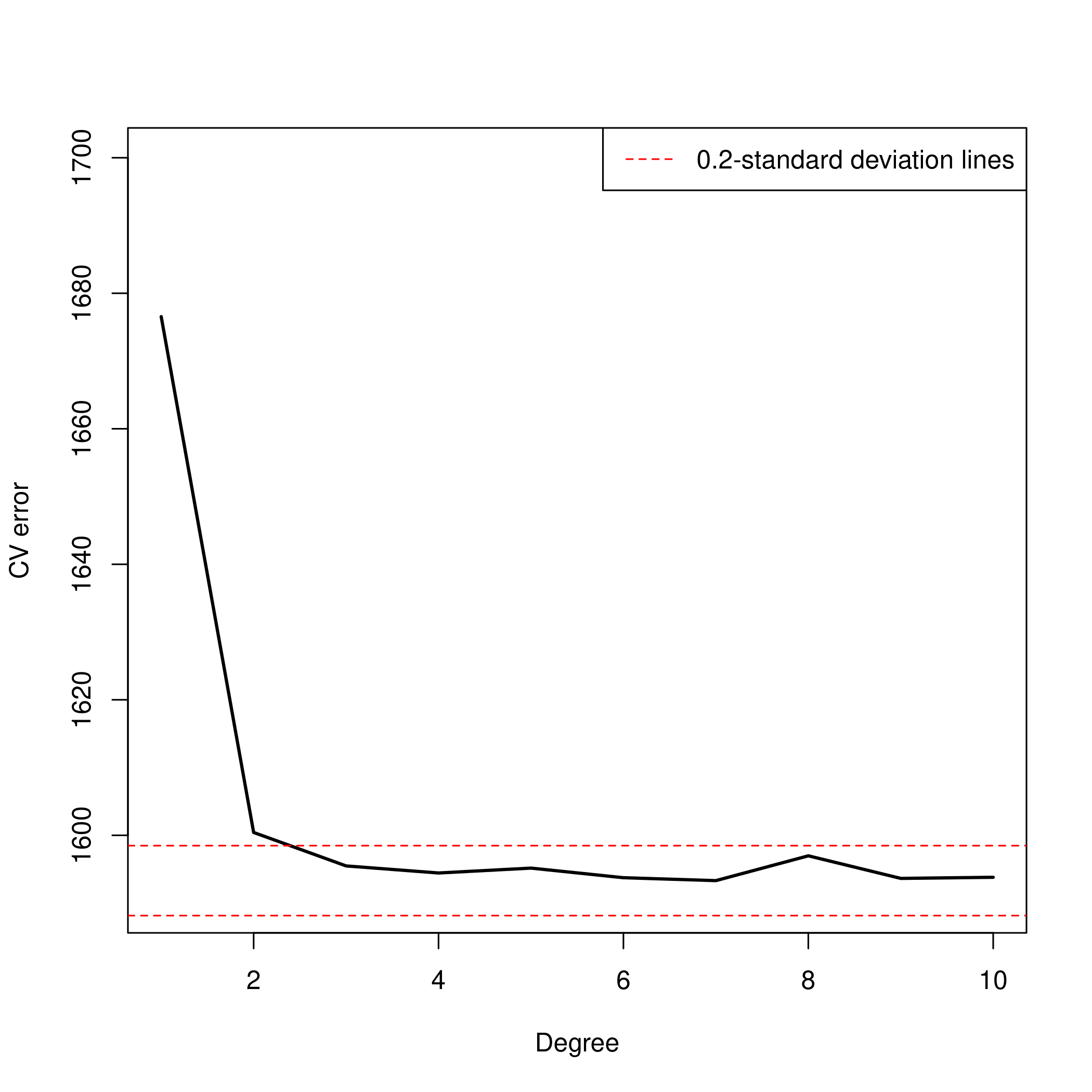
6plot(1:10, all.deltas, xlab="Degree", ylab="CV error", type="l", pch=20, lwd=2, ylim=c(1590, 1700))
7min.point = min(all.deltas)
8sd.points = sd(all.deltas)
9abline(h=min.point + 0.2 * sd.points, col="red", lty="dashed")
10abline(h=min.point - 0.2 * sd.points, col="red", lty="dashed")
11legend("topright", "0.2-standard deviation lines", lty="dashed", col="red")
1# ANOVA
2fits=list()
3for (i in 1:10) {
4 fits[[i]]=glm(wage~poly(age,i),data=wageDat)
5}
6anova(fits[[1]],fits[[2]],fits[[3]],fits[[4]],fits[[5]],
7 fits[[6]],fits[[7]],fits[[8]],fits[[9]],fits[[10]])
1## Analysis of Deviance Table
2##
3## Model 1: wage ~ poly(age, i)
4## Model 2: wage ~ poly(age, i)
5## Model 3: wage ~ poly(age, i)
6## Model 4: wage ~ poly(age, i)
7## Model 5: wage ~ poly(age, i)
8## Model 6: wage ~ poly(age, i)
9## Model 7: wage ~ poly(age, i)
10## Model 8: wage ~ poly(age, i)
11## Model 9: wage ~ poly(age, i)
12## Model 10: wage ~ poly(age, i)
13## Resid. Df Resid. Dev Df Deviance
14## 1 2998 5022216
15## 2 2997 4793430 1 228786
16## 3 2996 4777674 1 15756
17## 4 2995 4771604 1 6070
18## 5 2994 4770322 1 1283
19## 6 2993 4766389 1 3932
20## 7 2992 4763834 1 2555
21## 8 2991 4763707 1 127
22## 9 2990 4756703 1 7004
23## 10 2989 4756701 1 3
- The 4th degree looks the best at the moment
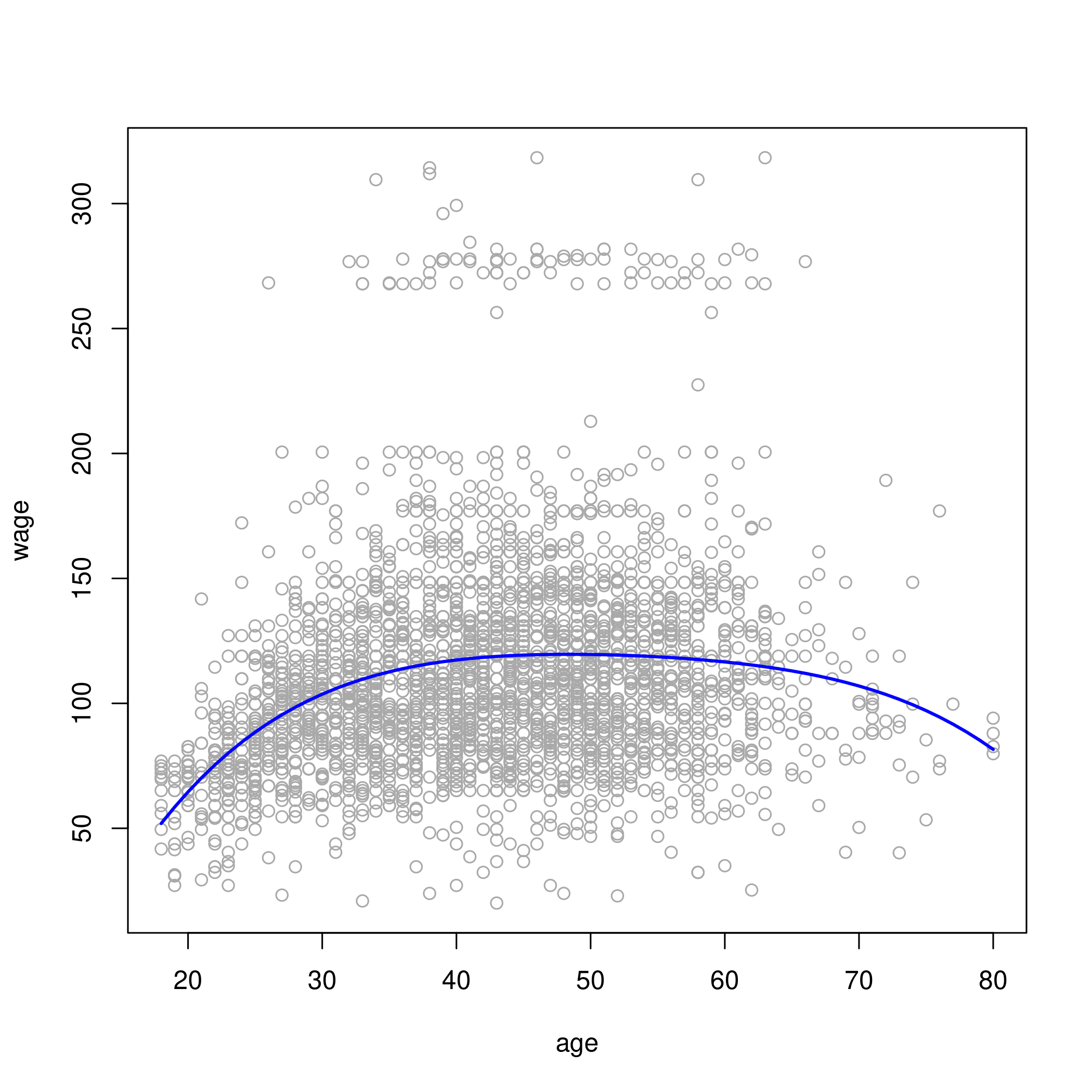
1# 3rd or 4th degrees look best based on ANOVA test
2# let's go with 4th degree fit
3plot(wage~age, data=wageDat, col="darkgrey")
4agelims = range(wageDat$age)
5age.grid = seq(from=agelims[1], to=agelims[2])
6lm.fit = lm(wage~poly(age, 4), data=wageDat)
7lm.pred = predict(lm.fit, data.frame(age=age.grid))
8lines(age.grid, lm.pred, col="blue", lwd=2)
b) Step function and cross-validation
1# cross-validation
2cv.error <- rep(0,9)
3for (i in 2:10) {
4 wageDat$age.cut <- cut(wageDat$age,i)
5 glm.fit <- glm(wage~age.cut, data=wageDat)
6 cv.error[i-1] <- cv.glm(wageDat, glm.fit, K=10)$delta[1] # [1]:std, [2]:bias-corrected
7}
8cv.error
1## [1] 1732.337 1682.978 1636.736 1635.600 1624.174 1610.688 1604.081 1612.005
2## [9] 1607.022
1cv.error
1## [1] 1732.337 1682.978 1636.736 1635.600 1624.174 1610.688 1604.081 1612.005
2## [9] 1607.022
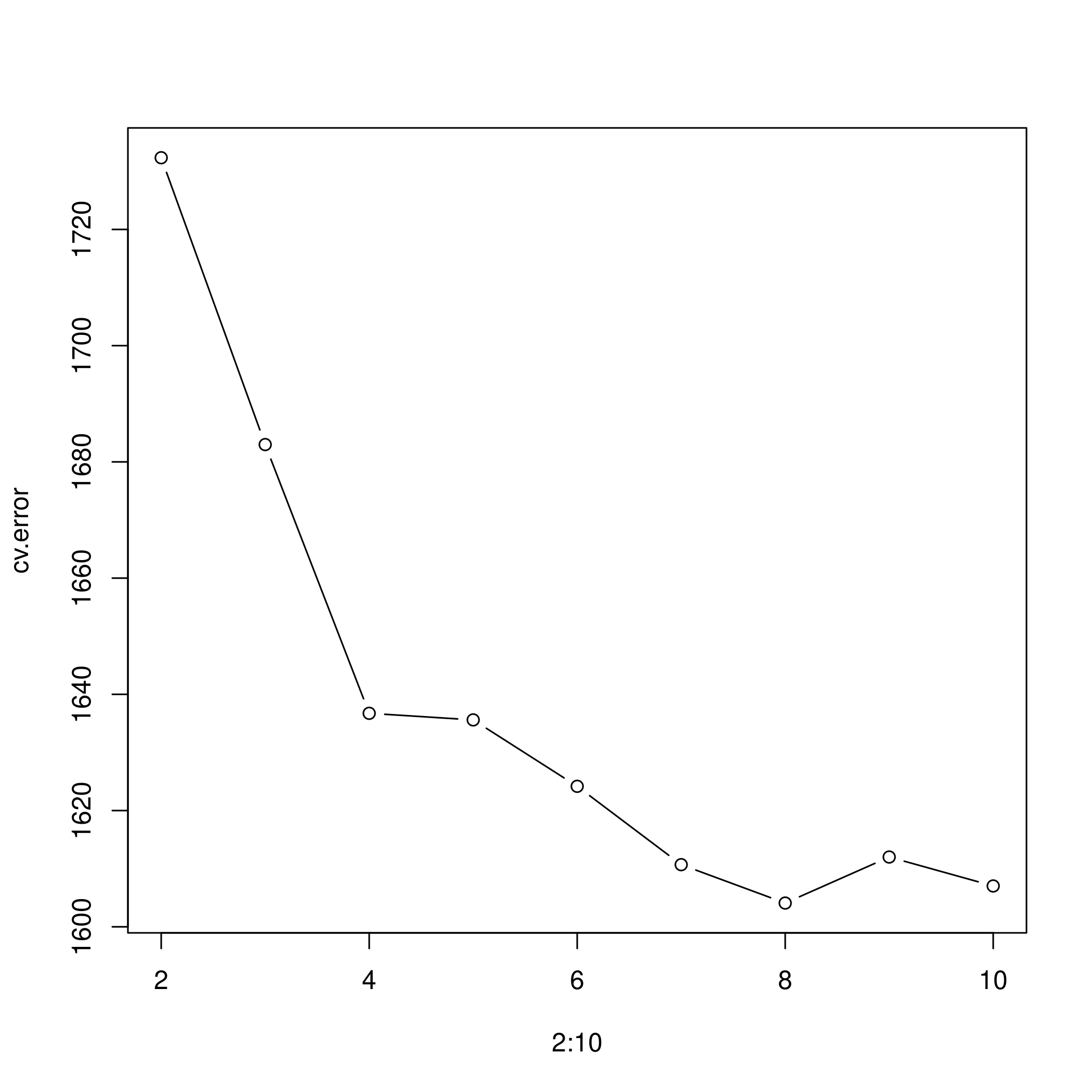
1plot(2:10, cv.error, type="b")
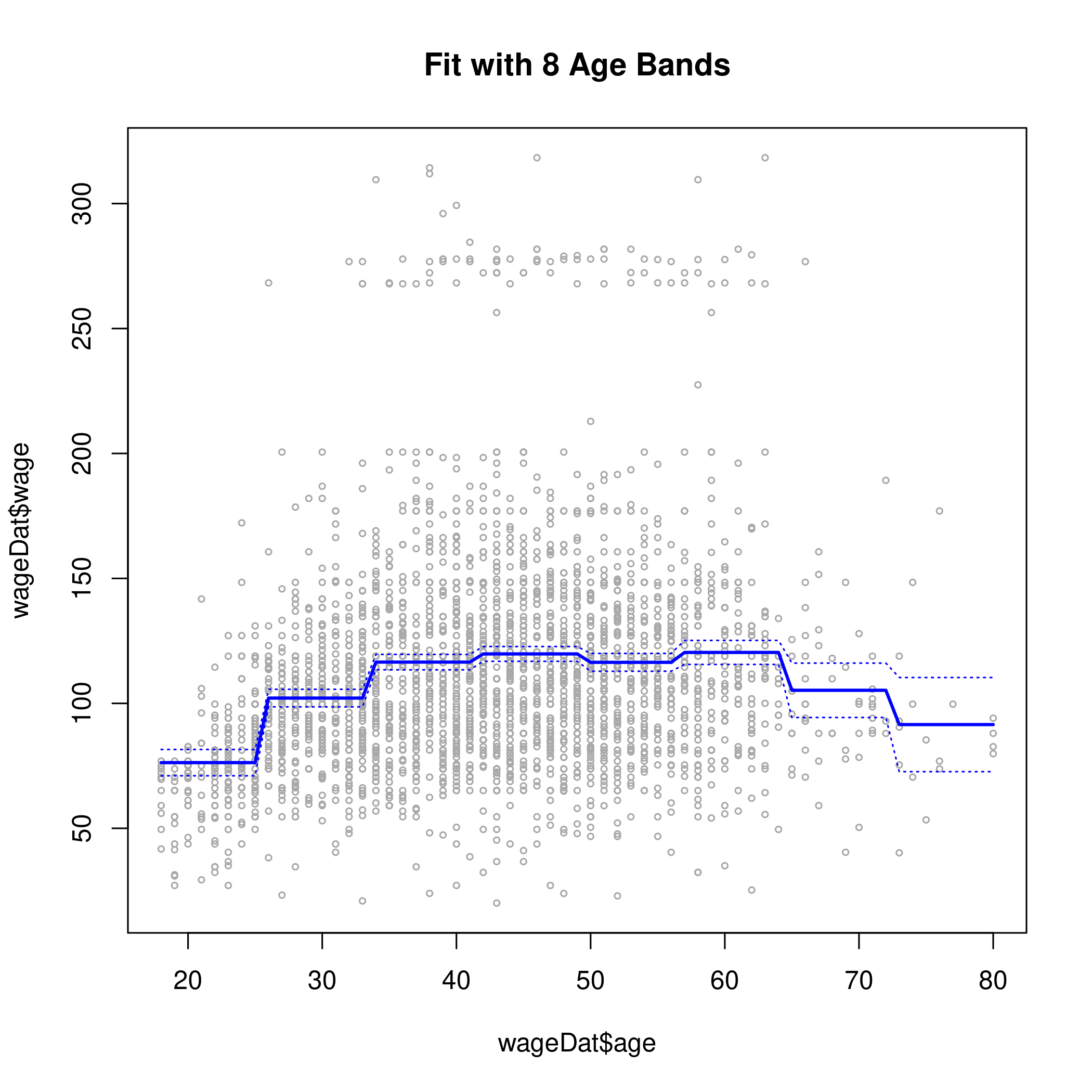
1cut.fit <- glm(wage~cut(age,8), data=wageDat)
2preds <- predict(cut.fit, newdata=list(age=age.grid), se=TRUE)
3se.bands <- preds$fit + cbind(2*preds$se.fit, -2*preds$se.fit)
4plot(wageDat$age, wageDat$wage, xlim=agelims, cex=0.5, col="darkgrey")
5title("Fit with 8 Age Bands")
6lines(age.grid, preds$fit, lwd=2, col="blue")
7matlines(age.grid, se.bands, lwd=1, col="blue", lty=3)
Question 7.8 - Page 299
Fit some of the non-linear models investigated in this chapter to the
Auto data set. Is there evidence for non-linear relationships in this
data set? Create some informative plots to justify your answer.
Answer
1autoDat<-ISLR::Auto
1autoDat %>% pivot_longer(-c(mpg,name),names_to="Params",values_to="Value") %>% ggplot(aes(x=mpg,y=Value)) +
2 geom_point() +
3 facet_wrap(~ Params, scales = "free_y")
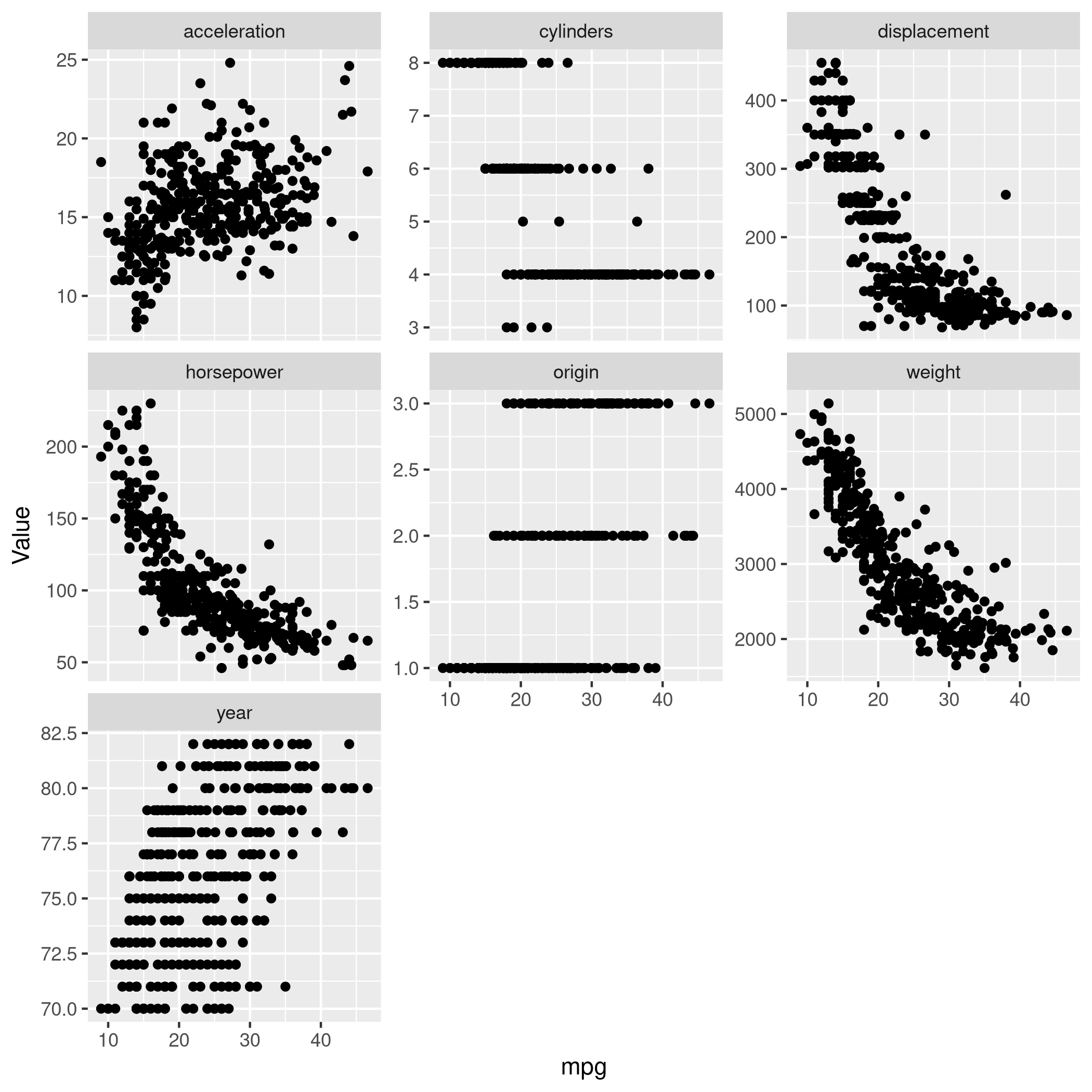
Very clearly there is a lot of non-linearity in the mpg data,
especially for acceleration, weight, displacement, horsepower.
1rss = rep(NA, 10)
2fits = list()
3for (d in 1:10) {
4 fits[[d]] = lm(mpg ~ poly(displacement, d), data = autoDat)
5 rss[d] = deviance(fits[[d]])
6}
7rss %>% print
1## [1] 8378.822 7412.263 7392.322 7391.722 7380.838 7270.746 7089.716 6917.401
2## [9] 6737.801 6610.190
1anova(fits[[1]],fits[[2]],fits[[3]],fits[[4]],fits[[5]],
2 fits[[6]],fits[[7]],fits[[8]],fits[[9]],fits[[10]])
1## Analysis of Variance Table
2##
3## Model 1: mpg ~ poly(displacement, d)
4## Model 2: mpg ~ poly(displacement, d)
5## Model 3: mpg ~ poly(displacement, d)
6## Model 4: mpg ~ poly(displacement, d)
7## Model 5: mpg ~ poly(displacement, d)
8## Model 6: mpg ~ poly(displacement, d)
9## Model 7: mpg ~ poly(displacement, d)
10## Model 8: mpg ~ poly(displacement, d)
11## Model 9: mpg ~ poly(displacement, d)
12## Model 10: mpg ~ poly(displacement, d)
13## Res.Df RSS Df Sum of Sq F Pr(>F)
14## 1 390 8378.8
15## 2 389 7412.3 1 966.56 55.7108 5.756e-13 ***
16## 3 388 7392.3 1 19.94 1.1494 0.284364
17## 4 387 7391.7 1 0.60 0.0346 0.852549
18## 5 386 7380.8 1 10.88 0.6273 0.428823
19## 6 385 7270.7 1 110.09 6.3455 0.012177 *
20## 7 384 7089.7 1 181.03 10.4343 0.001344 **
21## 8 383 6917.4 1 172.31 9.9319 0.001753 **
22## 9 382 6737.8 1 179.60 10.3518 0.001404 **
23## 10 381 6610.2 1 127.61 7.3553 0.006990 **
24## ---
25## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Confirming our visual indications, we see that the second degree models work well.
1library(glmnet)
1## Loading required package: Matrix
1##
2## Attaching package: 'Matrix'
1## The following objects are masked from 'package:tidyr':
2##
3## expand, pack, unpack
1## Loaded glmnet 3.0-2
1library(boot)
1cv.errs = rep(NA, 15)
2for (d in 1:15) {
3 fit = glm(mpg ~ poly(displacement, d), data = Auto)
4 cv.errs[d] = cv.glm(Auto, fit, K = 15)$delta[2]
5}
6which.min(cv.errs)
1## [1] 10
Strangely, we seem to have ended up with a ten variable model here.
1# Step functions
2cv.errs = rep(NA, 10)
3for (c in 2:10) {
4 Auto$dis.cut = cut(Auto$displacement, c)
5 fit = glm(mpg ~ dis.cut, data = Auto)
6 cv.errs[c] = cv.glm(Auto, fit, K = 10)$delta[2]
7}
8which.min(cv.errs) %>% print
1## [1] 9
1library(splines)
2cv.errs = rep(NA, 10)
3for (df in 3:10) {
4 fit = glm(mpg ~ ns(displacement, df = df), data = Auto)
5 cv.errs[df] = cv.glm(Auto, fit, K = 10)$delta[2]
6}
7which.min(cv.errs) %>% print
1## [1] 10
1library(gam)
1## Loading required package: foreach
1##
2## Attaching package: 'foreach'
1## The following objects are masked from 'package:purrr':
2##
3## accumulate, when
1## Loaded gam 1.16.1
1# GAMs
2fit = gam(mpg ~ s(displacement, 4) + s(horsepower, 4), data = Auto)
1## Warning in model.matrix.default(mt, mf, contrasts): non-list contrasts argument
2## ignored
1summary(fit)
1##
2## Call: gam(formula = mpg ~ s(displacement, 4) + s(horsepower, 4), data = Auto)
3## Deviance Residuals:
4## Min 1Q Median 3Q Max
5## -11.2982 -2.1592 -0.4394 2.1247 17.0946
6##
7## (Dispersion Parameter for gaussian family taken to be 15.3543)
8##
9## Null Deviance: 23818.99 on 391 degrees of freedom
10## Residual Deviance: 5880.697 on 382.9999 degrees of freedom
11## AIC: 2194.05
12##
13## Number of Local Scoring Iterations: 2
14##
15## Anova for Parametric Effects
16## Df Sum Sq Mean Sq F value Pr(>F)
17## s(displacement, 4) 1 15254.9 15254.9 993.524 < 2e-16 ***
18## s(horsepower, 4) 1 1038.4 1038.4 67.632 3.1e-15 ***
19## Residuals 383 5880.7 15.4
20## ---
21## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
22##
23## Anova for Nonparametric Effects
24## Npar Df Npar F Pr(F)
25## (Intercept)
26## s(displacement, 4) 3 13.613 1.863e-08 ***
27## s(horsepower, 4) 3 15.606 1.349e-09 ***
28## ---
29## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Question 7.9 - Pages 299-300
This question uses the variables dis (the weighted mean of distances
to five Boston employment centers) and nox (nitrogen oxides
concentration in parts per 10 million) from the Boston data. We will
treat dis as the predictor and nox as the response.
(a) Use the poly() function to fit a cubic polynomial regression to
predict nox using dis. Report the regression output, and plot the
resulting data and polynomial fits.
(b) Plot the polynomial fits for a range of different polynomial degrees (say, from 1 to 10), and report the associated residual sum of squares.
(c) Perform cross-validation or another approach to select the optimal degree for the polynomial, and explain your results.
(d) Use the bs() function to fit a regression spline to predict nox
using dis. Report the output for the fit using four degrees of
freedom. How did you choose the knots? Plot the resulting fit.
(e) Now fit a regression spline for a range of degrees of freedom, and plot the resulting fits and report the resulting RSS. Describe the results obtained.
(f) Perform cross-validation or another approach in order to select the best degrees of freedom for a regression spline on this data. Describe your results.
Answer
1boston<-MASS::Boston
2boston %>% str %>% print
1## 'data.frame': 506 obs. of 14 variables:
2## $ crim : num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
3## $ zn : num 18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
4## $ indus : num 2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
5## $ chas : int 0 0 0 0 0 0 0 0 0 0 ...
6## $ nox : num 0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
7## $ rm : num 6.58 6.42 7.18 7 7.15 ...
8## $ age : num 65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
9## $ dis : num 4.09 4.97 4.97 6.06 6.06 ...
10## $ rad : int 1 2 2 3 3 3 5 5 5 5 ...
11## $ tax : num 296 242 242 222 222 222 311 311 311 311 ...
12## $ ptratio: num 15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
13## $ black : num 397 397 393 395 397 ...
14## $ lstat : num 4.98 9.14 4.03 2.94 5.33 ...
15## $ medv : num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...
16## NULL
1boston %>% summary %>% print
1## crim zn indus chas
2## Min. : 0.00632 Min. : 0.00 Min. : 0.46 Min. :0.00000
3## 1st Qu.: 0.08204 1st Qu.: 0.00 1st Qu.: 5.19 1st Qu.:0.00000
4## Median : 0.25651 Median : 0.00 Median : 9.69 Median :0.00000
5## Mean : 3.61352 Mean : 11.36 Mean :11.14 Mean :0.06917
6## 3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10 3rd Qu.:0.00000
7## Max. :88.97620 Max. :100.00 Max. :27.74 Max. :1.00000
8## nox rm age dis
9## Min. :0.3850 Min. :3.561 Min. : 2.90 Min. : 1.130
10## 1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 45.02 1st Qu.: 2.100
11## Median :0.5380 Median :6.208 Median : 77.50 Median : 3.207
12## Mean :0.5547 Mean :6.285 Mean : 68.57 Mean : 3.795
13## 3rd Qu.:0.6240 3rd Qu.:6.623 3rd Qu.: 94.08 3rd Qu.: 5.188
14## Max. :0.8710 Max. :8.780 Max. :100.00 Max. :12.127
15## rad tax ptratio black
16## Min. : 1.000 Min. :187.0 Min. :12.60 Min. : 0.32
17## 1st Qu.: 4.000 1st Qu.:279.0 1st Qu.:17.40 1st Qu.:375.38
18## Median : 5.000 Median :330.0 Median :19.05 Median :391.44
19## Mean : 9.549 Mean :408.2 Mean :18.46 Mean :356.67
20## 3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.23
21## Max. :24.000 Max. :711.0 Max. :22.00 Max. :396.90
22## lstat medv
23## Min. : 1.73 Min. : 5.00
24## 1st Qu.: 6.95 1st Qu.:17.02
25## Median :11.36 Median :21.20
26## Mean :12.65 Mean :22.53
27## 3rd Qu.:16.95 3rd Qu.:25.00
28## Max. :37.97 Max. :50.00
1boston %>% sapply(unique) %>% sapply(length) %>% print
1## crim zn indus chas nox rm age dis rad tax
2## 504 26 76 2 81 446 356 412 9 66
3## ptratio black lstat medv
4## 46 357 455 229
a) Polynomial
1fit.03 <- lm(nox~poly(dis,3), data=boston)
2dislims <- range(boston$dis)
3dis.grid <- seq(dislims[1], dislims[2], 0.1)
4preds <- predict(fit.03, newdata=list(dis=dis.grid), se=TRUE)
5se.bands <- preds$fit + cbind(2*preds$se.fit, -2*preds$se.fit)
6par(mfrow=c(1,1), mar=c(4.5,4.5,1,1), oma=c(0,0,4,0))
7plot(boston$dis, boston$nox, xlim=dislims, cex=0.5, col="darkgrey")
8title("Degree 3 Polynomial Fit")
9lines(dis.grid, preds$fit, lwd=2, col="blue")
10matlines(dis.grid, se.bands, lwd=1, col="blue", lty=3)
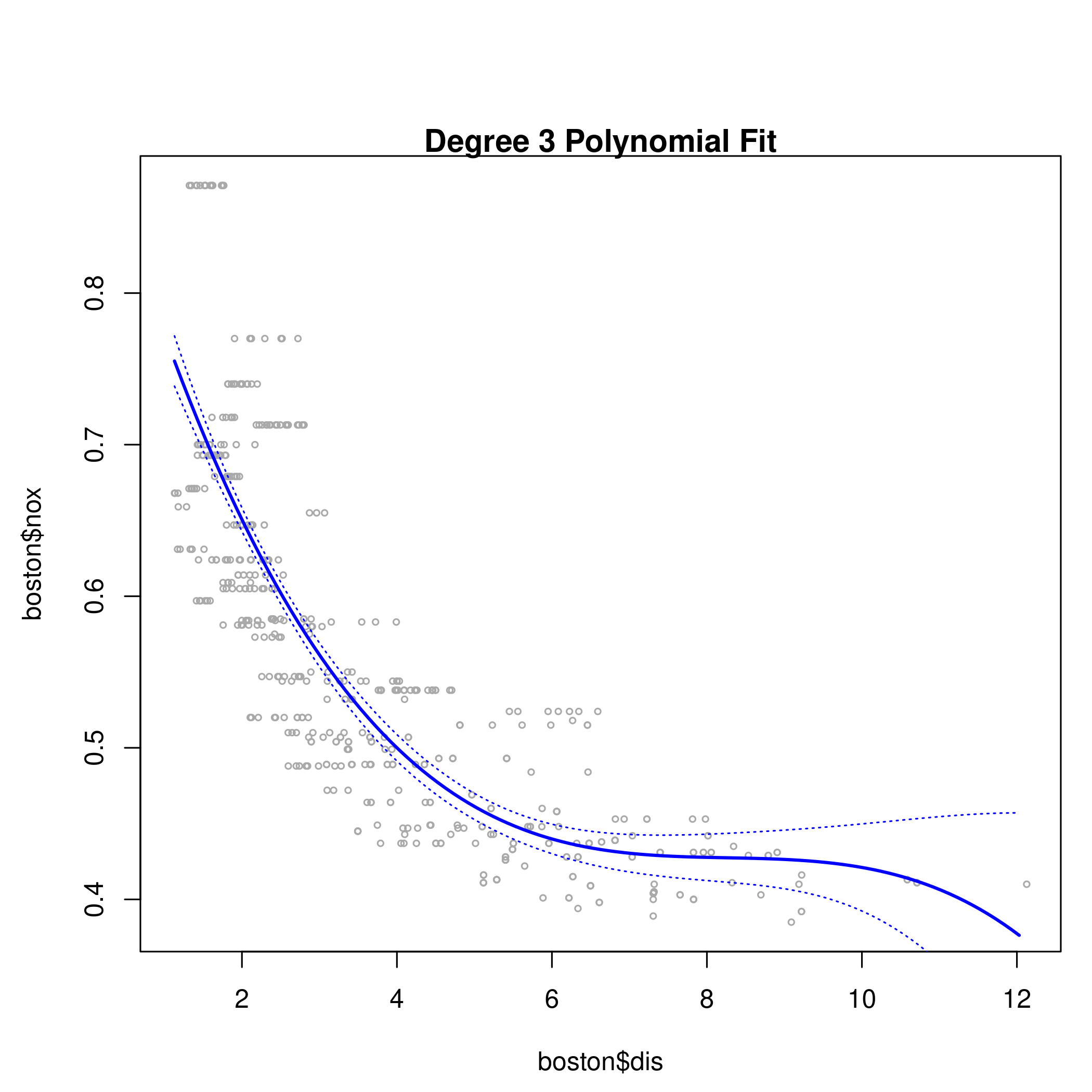
1summary(fit.03)
1##
2## Call:
3## lm(formula = nox ~ poly(dis, 3), data = boston)
4##
5## Residuals:
6## Min 1Q Median 3Q Max
7## -0.121130 -0.040619 -0.009738 0.023385 0.194904
8##
9## Coefficients:
10## Estimate Std. Error t value Pr(>|t|)
11## (Intercept) 0.554695 0.002759 201.021 < 2e-16 ***
12## poly(dis, 3)1 -2.003096 0.062071 -32.271 < 2e-16 ***
13## poly(dis, 3)2 0.856330 0.062071 13.796 < 2e-16 ***
14## poly(dis, 3)3 -0.318049 0.062071 -5.124 4.27e-07 ***
15## ---
16## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
17##
18## Residual standard error: 0.06207 on 502 degrees of freedom
19## Multiple R-squared: 0.7148, Adjusted R-squared: 0.7131
20## F-statistic: 419.3 on 3 and 502 DF, p-value: < 2.2e-16
b) Multiple Polynomials
1rss.error <- rep(0,10)
2for (i in 1:10) {
3 lm.fit <- lm(nox~poly(dis,i), data=boston)
4 rss.error[i] <- sum(lm.fit$residuals^2)
5}
6rss.error
1## [1] 2.768563 2.035262 1.934107 1.932981 1.915290 1.878257 1.849484 1.835630
2## [9] 1.833331 1.832171
1plot(rss.error, type="b")
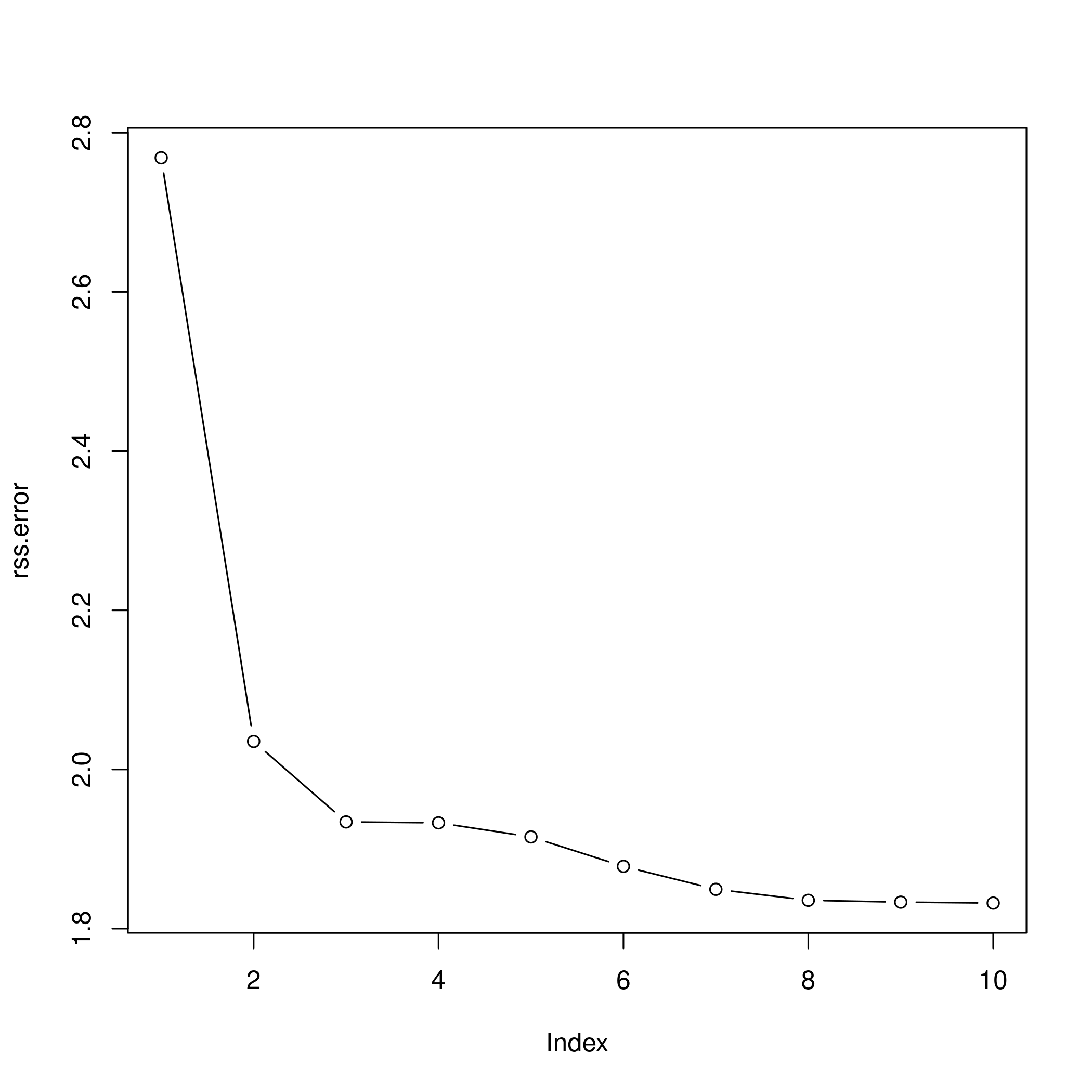
c) Cross validation and polynomial selection
1require(boot)
2set.seed(1)
3cv.error <- rep(0,10)
4for (i in 1:10) {
5 glm.fit <- glm(nox~poly(dis,i), data=boston)
6 cv.error[i] <- cv.glm(boston, glm.fit, K=10)$delta[1] # [1]:std, [2]:bias-corrected
7}
8cv.error
1## [1] 0.005558263 0.004085706 0.003876521 0.003863342 0.004237452 0.005686862
2## [7] 0.010278897 0.006810868 0.033308607 0.004075599
1plot(cv.error, type="b")
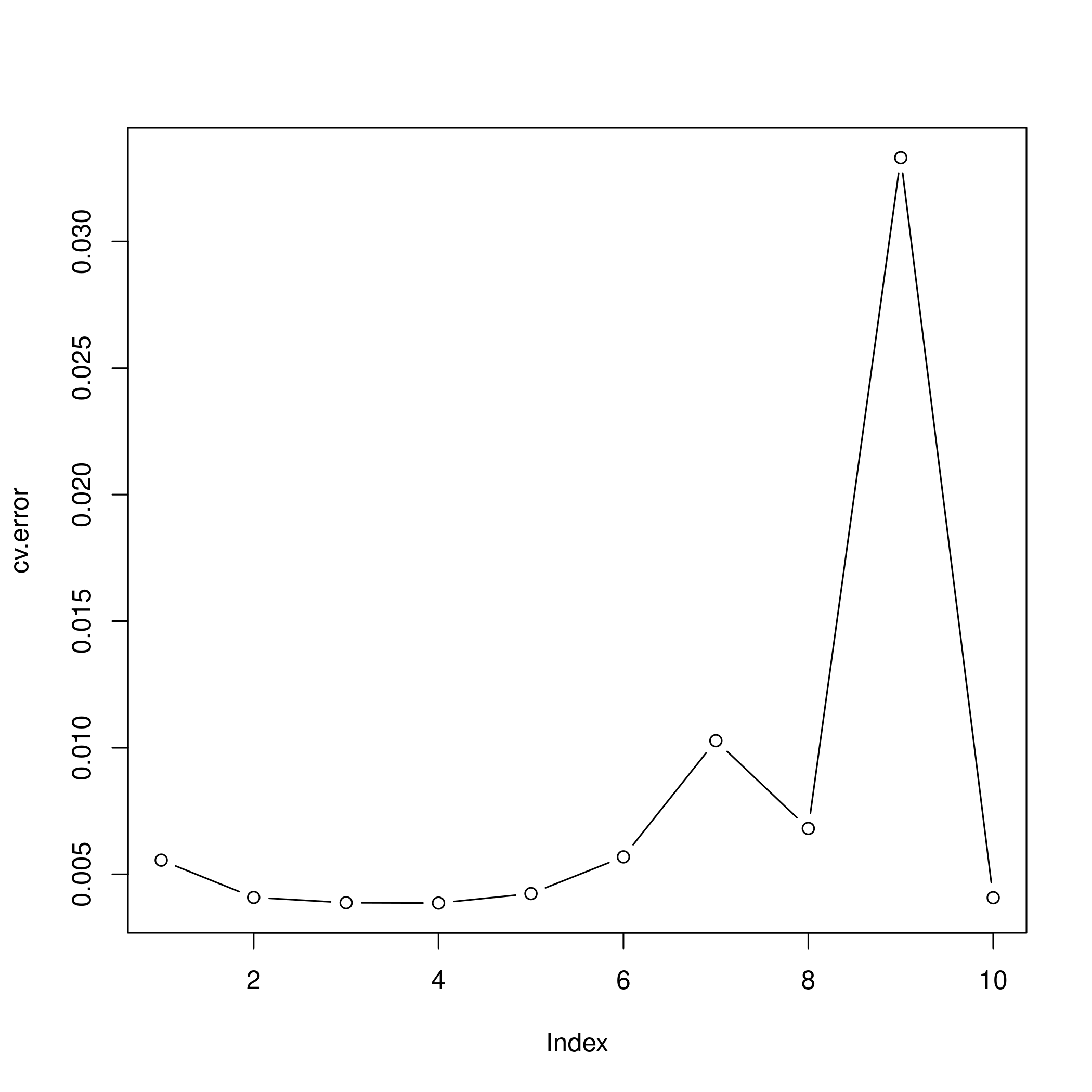
- I feel like the second degree fit would be the most reasonable, though the fourth degree seems to be doing well.
d) Regression spline
1fit.sp <- lm(nox~bs(dis, df=4), data=boston)
2pred <- predict(fit.sp, newdata=list(dis=dis.grid), se=T)
3plot(boston$dis, boston$nox, col="gray")
4lines(dis.grid, pred$fit, lwd=2)
5lines(dis.grid, pred$fit+2*pred$se, lty="dashed")
6lines(dis.grid, pred$fit-2*pred$se, lty="dashed")
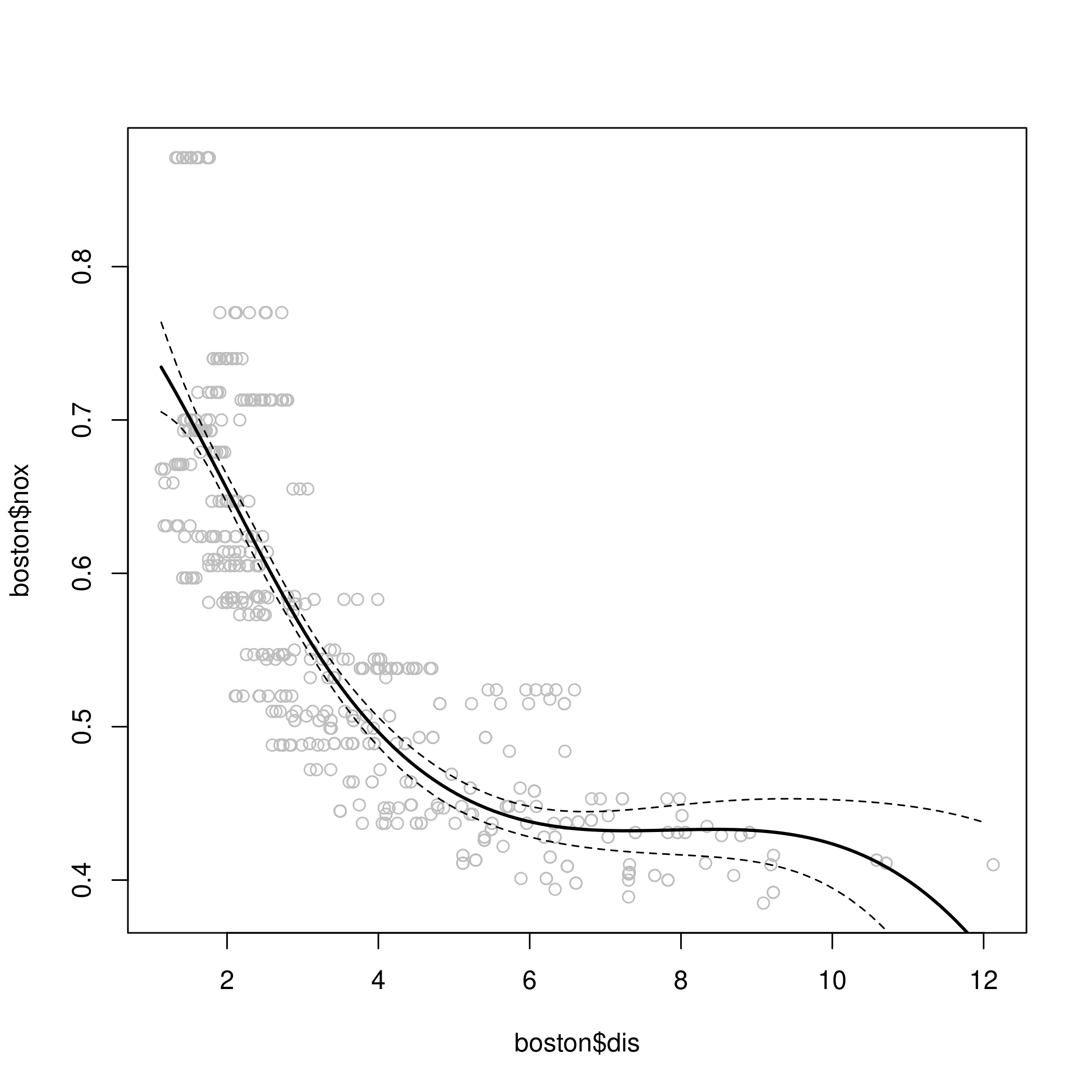
1# set df to select knots at uniform quantiles of `dis`
2attr(bs(boston$dis,df=4),"knots") # only 1 knot at 50th percentile
1## 50%
2## 3.20745
e) Range of regression splines
1rss.error <- rep(0,7)
2for (i in 4:10) {
3 fit.sp <- lm(nox~bs(dis, df=i), data=boston)
4 rss.error[i-3] <- sum(fit.sp$residuals^2)
5}
6rss.error
1## [1] 1.922775 1.840173 1.833966 1.829884 1.816995 1.825653 1.792535
1plot(4:10, rss.error, type="b")
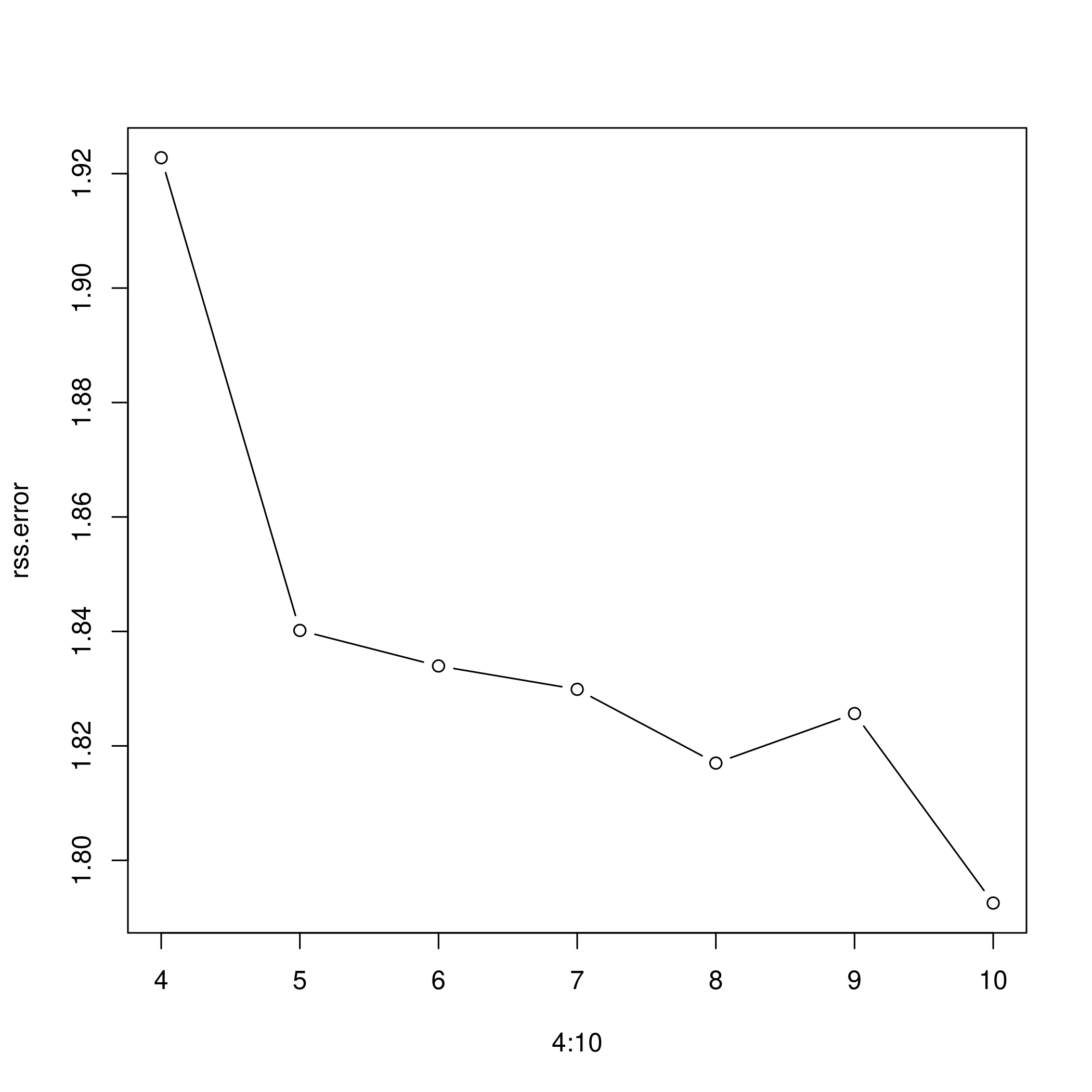
- As the model gains more degrees of freedom, it tends to over fit to the training data better
f) Cross validation for best spline
1cv.error <- rep(0,7)
2for (i in 4:10) {
3 glm.fit <- glm(nox~bs(dis, df=i), data=boston)
4 cv.error[i-3] <- cv.glm(boston, glm.fit, K=10)$delta[1]
5}
1## Warning in bs(dis, degree = 3L, knots = c(`50%` = 3.1523), Boundary.knots =
2## c(1.1296, : some 'x' values beyond boundary knots may cause ill-conditioned
3## bases
4
5## Warning in bs(dis, degree = 3L, knots = c(`50%` = 3.1523), Boundary.knots =
6## c(1.1296, : some 'x' values beyond boundary knots may cause ill-conditioned
7## bases
1## Warning in bs(dis, degree = 3L, knots = c(`50%` = 3.2157), Boundary.knots =
2## c(1.137, : some 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`50%` = 3.2157), Boundary.knots =
5## c(1.137, : some 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`33.33333%` = 2.35953333333333, : some
2## 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`33.33333%` = 2.35953333333333, : some
5## 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`33.33333%` = 2.38403333333333, : some
2## 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`33.33333%` = 2.38403333333333, : some
5## 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`25%` = 2.07945, `50%` = 3.1323, :
2## some 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`25%` = 2.07945, `50%` = 3.1323, :
5## some 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`25%` = 2.1103, `50%` = 3.2797, : some
2## 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`25%` = 2.1103, `50%` = 3.2797, : some
5## 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`20%` = 1.9682, `40%` = 2.7147, : some
2## 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`20%` = 1.9682, `40%` = 2.7147, : some
5## 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`20%` = 1.95434, `40%` = 2.59666, :
2## some 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`20%` = 1.95434, `40%` = 2.59666, :
5## some 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`16.66667%` = 1.82203333333333, : some
2## 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`16.66667%` = 1.82203333333333, : some
5## 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`16.66667%` = 1.8226, `33.33333%` =
2## 2.3817, : some 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`16.66667%` = 1.8226, `33.33333%` =
5## 2.3817, : some 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`14.28571%` = 1.7936, `28.57143%`
2## = 2.16972857142857, : some 'x' values beyond boundary knots may cause ill-
3## conditioned bases
4
5## Warning in bs(dis, degree = 3L, knots = c(`14.28571%` = 1.7936, `28.57143%`
6## = 2.16972857142857, : some 'x' values beyond boundary knots may cause ill-
7## conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`12.5%` = 1.754625, `25%` = 2.10215, :
2## some 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`12.5%` = 1.754625, `25%` = 2.10215, :
5## some 'x' values beyond boundary knots may cause ill-conditioned bases
1## Warning in bs(dis, degree = 3L, knots = c(`12.5%` = 1.751575, `25%` = 2.08755, :
2## some 'x' values beyond boundary knots may cause ill-conditioned bases
3
4## Warning in bs(dis, degree = 3L, knots = c(`12.5%` = 1.751575, `25%` = 2.08755, :
5## some 'x' values beyond boundary knots may cause ill-conditioned bases
1cv.error
1## [1] 0.003898810 0.003694675 0.003732665 0.003766202 0.003716389 0.003723126
2## [7] 0.003727358
1plot(4:10, cv.error, type="b")
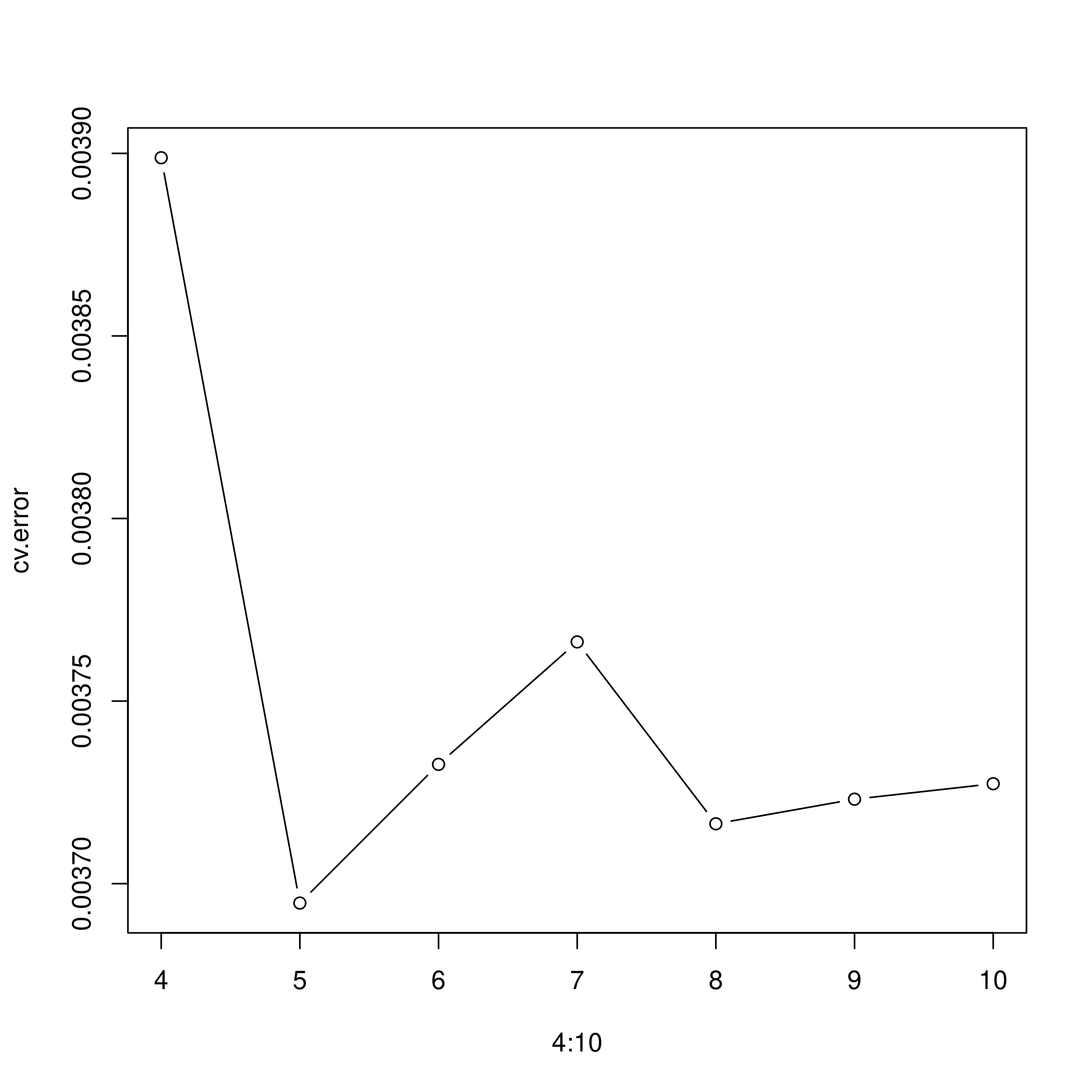
- A fifth degree polynomial is clearly indicated
Question 10 - Page 300
This question relates to the College data set.
(a) Split the data into a training set and a test set. Using out-of-state tuition as the response and the other variables as the predictors, perform forward stepwise selection on the training set in order to identify a satisfactory model that uses just a subset of the predictors.
(b) Fit a GAM on the training data, using out-of-state tuition as the response and the features selected in the previous step as the predictors. Plot the results, and explain your findings.
(c) Evaluate the model obtained on the test set, and explain the results obtained.
(d) For which variables, if any, is there evidence of a non-linear relationship with the response?
Answer
1colDat<-ISLR::College
2colDat %>% str %>% print
1## 'data.frame': 777 obs. of 18 variables:
2## $ Private : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 2 2 2 2 2 ...
3## $ Apps : num 1660 2186 1428 417 193 ...
4## $ Accept : num 1232 1924 1097 349 146 ...
5## $ Enroll : num 721 512 336 137 55 158 103 489 227 172 ...
6## $ Top10perc : num 23 16 22 60 16 38 17 37 30 21 ...
7## $ Top25perc : num 52 29 50 89 44 62 45 68 63 44 ...
8## $ F.Undergrad: num 2885 2683 1036 510 249 ...
9## $ P.Undergrad: num 537 1227 99 63 869 ...
10## $ Outstate : num 7440 12280 11250 12960 7560 ...
11## $ Room.Board : num 3300 6450 3750 5450 4120 ...
12## $ Books : num 450 750 400 450 800 500 500 450 300 660 ...
13## $ Personal : num 2200 1500 1165 875 1500 ...
14## $ PhD : num 70 29 53 92 76 67 90 89 79 40 ...
15## $ Terminal : num 78 30 66 97 72 73 93 100 84 41 ...
16## $ S.F.Ratio : num 18.1 12.2 12.9 7.7 11.9 9.4 11.5 13.7 11.3 11.5 ...
17## $ perc.alumni: num 12 16 30 37 2 11 26 37 23 15 ...
18## $ Expend : num 7041 10527 8735 19016 10922 ...
19## $ Grad.Rate : num 60 56 54 59 15 55 63 73 80 52 ...
20## NULL
1colDat %>% summary %>% print
1## Private Apps Accept Enroll Top10perc
2## No :212 Min. : 81 Min. : 72 Min. : 35 Min. : 1.00
3## Yes:565 1st Qu.: 776 1st Qu.: 604 1st Qu.: 242 1st Qu.:15.00
4## Median : 1558 Median : 1110 Median : 434 Median :23.00
5## Mean : 3002 Mean : 2019 Mean : 780 Mean :27.56
6## 3rd Qu.: 3624 3rd Qu.: 2424 3rd Qu.: 902 3rd Qu.:35.00
7## Max. :48094 Max. :26330 Max. :6392 Max. :96.00
8## Top25perc F.Undergrad P.Undergrad Outstate
9## Min. : 9.0 Min. : 139 Min. : 1.0 Min. : 2340
10## 1st Qu.: 41.0 1st Qu.: 992 1st Qu.: 95.0 1st Qu.: 7320
11## Median : 54.0 Median : 1707 Median : 353.0 Median : 9990
12## Mean : 55.8 Mean : 3700 Mean : 855.3 Mean :10441
13## 3rd Qu.: 69.0 3rd Qu.: 4005 3rd Qu.: 967.0 3rd Qu.:12925
14## Max. :100.0 Max. :31643 Max. :21836.0 Max. :21700
15## Room.Board Books Personal PhD
16## Min. :1780 Min. : 96.0 Min. : 250 Min. : 8.00
17## 1st Qu.:3597 1st Qu.: 470.0 1st Qu.: 850 1st Qu.: 62.00
18## Median :4200 Median : 500.0 Median :1200 Median : 75.00
19## Mean :4358 Mean : 549.4 Mean :1341 Mean : 72.66
20## 3rd Qu.:5050 3rd Qu.: 600.0 3rd Qu.:1700 3rd Qu.: 85.00
21## Max. :8124 Max. :2340.0 Max. :6800 Max. :103.00
22## Terminal S.F.Ratio perc.alumni Expend
23## Min. : 24.0 Min. : 2.50 Min. : 0.00 Min. : 3186
24## 1st Qu.: 71.0 1st Qu.:11.50 1st Qu.:13.00 1st Qu.: 6751
25## Median : 82.0 Median :13.60 Median :21.00 Median : 8377
26## Mean : 79.7 Mean :14.09 Mean :22.74 Mean : 9660
27## 3rd Qu.: 92.0 3rd Qu.:16.50 3rd Qu.:31.00 3rd Qu.:10830
28## Max. :100.0 Max. :39.80 Max. :64.00 Max. :56233
29## Grad.Rate
30## Min. : 10.00
31## 1st Qu.: 53.00
32## Median : 65.00
33## Mean : 65.46
34## 3rd Qu.: 78.00
35## Max. :118.00
1colDat %>% sapply(unique) %>% sapply(length) %>% print
1## Private Apps Accept Enroll Top10perc Top25perc
2## 2 711 693 581 82 89
3## F.Undergrad P.Undergrad Outstate Room.Board Books Personal
4## 714 566 640 553 122 294
5## PhD Terminal S.F.Ratio perc.alumni Expend Grad.Rate
6## 78 65 173 61 744 81
1plotLEAP=function(leapObj){
2 par(mfrow = c(2,2))
3 bar2=which.max(leapObj$adjr2)
4 bbic=which.min(leapObj$bic)
5 bcp=which.min(leapObj$cp)
6 plot(leapObj$rss,xlab="Number of variables",ylab="RSS",type="b")
7 plot(leapObj$adjr2,xlab="Number of variables",ylab=TeX("Adjusted R^2"),type="b")
8 points(bar2,leapObj$adjr2[bar2],col="green",cex=2,pch=20)
9 plot(leapObj$bic,xlab="Number of variables",ylab=TeX("BIC"),type="b")
10 points(bbic,leapObj$bic[bbic],col="blue",cex=2,pch=20)
11 plot(leapObj$cp,xlab="Number of variables",ylab=TeX("C_p"),type="b")
12 points(bcp,leapObj$cp[bcp],col="red",cex=2,pch=20)
13}
a) Train test
1train_ind = sample(colDat %>% nrow,100)
2test_ind = setdiff(seq_len(colDat %>% nrow), train_ind)
Best subset selection
1train_set<-colDat[train_ind,]
2test_set<-colDat[-train_ind,]
1library(leaps)
1modelFit<-regsubsets(Outstate~.,data=colDat,nvmax=20)
2modelFit %>% summary %>% print
1## Subset selection object
2## Call: regsubsets.formula(Outstate ~ ., data = colDat, nvmax = 20)
3## 17 Variables (and intercept)
4## Forced in Forced out
5## PrivateYes FALSE FALSE
6## Apps FALSE FALSE
7## Accept FALSE FALSE
8## Enroll FALSE FALSE
9## Top10perc FALSE FALSE
10## Top25perc FALSE FALSE
11## F.Undergrad FALSE FALSE
12## P.Undergrad FALSE FALSE
13## Room.Board FALSE FALSE
14## Books FALSE FALSE
15## Personal FALSE FALSE
16## PhD FALSE FALSE
17## Terminal FALSE FALSE
18## S.F.Ratio FALSE FALSE
19## perc.alumni FALSE FALSE
20## Expend FALSE FALSE
21## Grad.Rate FALSE FALSE
22## 1 subsets of each size up to 17
23## Selection Algorithm: exhaustive
24## PrivateYes Apps Accept Enroll Top10perc Top25perc F.Undergrad
25## 1 ( 1 ) " " " " " " " " " " " " " "
26## 2 ( 1 ) "*" " " " " " " " " " " " "
27## 3 ( 1 ) "*" " " " " " " " " " " " "
28## 4 ( 1 ) "*" " " " " " " " " " " " "
29## 5 ( 1 ) "*" " " " " " " " " " " " "
30## 6 ( 1 ) "*" " " " " " " " " " " " "
31## 7 ( 1 ) "*" " " " " " " " " " " " "
32## 8 ( 1 ) "*" " " "*" " " " " " " "*"
33## 9 ( 1 ) "*" "*" "*" " " " " " " "*"
34## 10 ( 1 ) "*" "*" "*" " " "*" " " "*"
35## 11 ( 1 ) "*" "*" "*" " " "*" " " "*"
36## 12 ( 1 ) "*" "*" "*" " " "*" " " "*"
37## 13 ( 1 ) "*" "*" "*" "*" "*" " " "*"
38## 14 ( 1 ) "*" "*" "*" "*" "*" " " "*"
39## 15 ( 1 ) "*" "*" "*" "*" "*" " " "*"
40## 16 ( 1 ) "*" "*" "*" "*" "*" "*" "*"
41## 17 ( 1 ) "*" "*" "*" "*" "*" "*" "*"
42## P.Undergrad Room.Board Books Personal PhD Terminal S.F.Ratio
43## 1 ( 1 ) " " " " " " " " " " " " " "
44## 2 ( 1 ) " " " " " " " " " " " " " "
45## 3 ( 1 ) " " "*" " " " " " " " " " "
46## 4 ( 1 ) " " "*" " " " " " " " " " "
47## 5 ( 1 ) " " "*" " " " " "*" " " " "
48## 6 ( 1 ) " " "*" " " " " " " "*" " "
49## 7 ( 1 ) " " "*" " " "*" " " "*" " "
50## 8 ( 1 ) " " "*" " " " " " " "*" " "
51## 9 ( 1 ) " " "*" " " " " " " "*" " "
52## 10 ( 1 ) " " "*" " " " " " " "*" " "
53## 11 ( 1 ) " " "*" " " "*" " " "*" " "
54## 12 ( 1 ) " " "*" " " "*" " " "*" "*"
55## 13 ( 1 ) " " "*" " " "*" " " "*" "*"
56## 14 ( 1 ) " " "*" " " "*" "*" "*" "*"
57## 15 ( 1 ) " " "*" "*" "*" "*" "*" "*"
58## 16 ( 1 ) " " "*" "*" "*" "*" "*" "*"
59## 17 ( 1 ) "*" "*" "*" "*" "*" "*" "*"
60## perc.alumni Expend Grad.Rate
61## 1 ( 1 ) " " "*" " "
62## 2 ( 1 ) " " "*" " "
63## 3 ( 1 ) " " "*" " "
64## 4 ( 1 ) "*" "*" " "
65## 5 ( 1 ) "*" "*" " "
66## 6 ( 1 ) "*" "*" "*"
67## 7 ( 1 ) "*" "*" "*"
68## 8 ( 1 ) "*" "*" "*"
69## 9 ( 1 ) "*" "*" "*"
70## 10 ( 1 ) "*" "*" "*"
71## 11 ( 1 ) "*" "*" "*"
72## 12 ( 1 ) "*" "*" "*"
73## 13 ( 1 ) "*" "*" "*"
74## 14 ( 1 ) "*" "*" "*"
75## 15 ( 1 ) "*" "*" "*"
76## 16 ( 1 ) "*" "*" "*"
77## 17 ( 1 ) "*" "*" "*"
We might want to take a look at these.
1par(mfrow=c(2,2))
2plot(modelFit)
3plot(modelFit,scale='Cp')
4plot(modelFit,scale='r2')
5plot(modelFit,scale='adjr2')
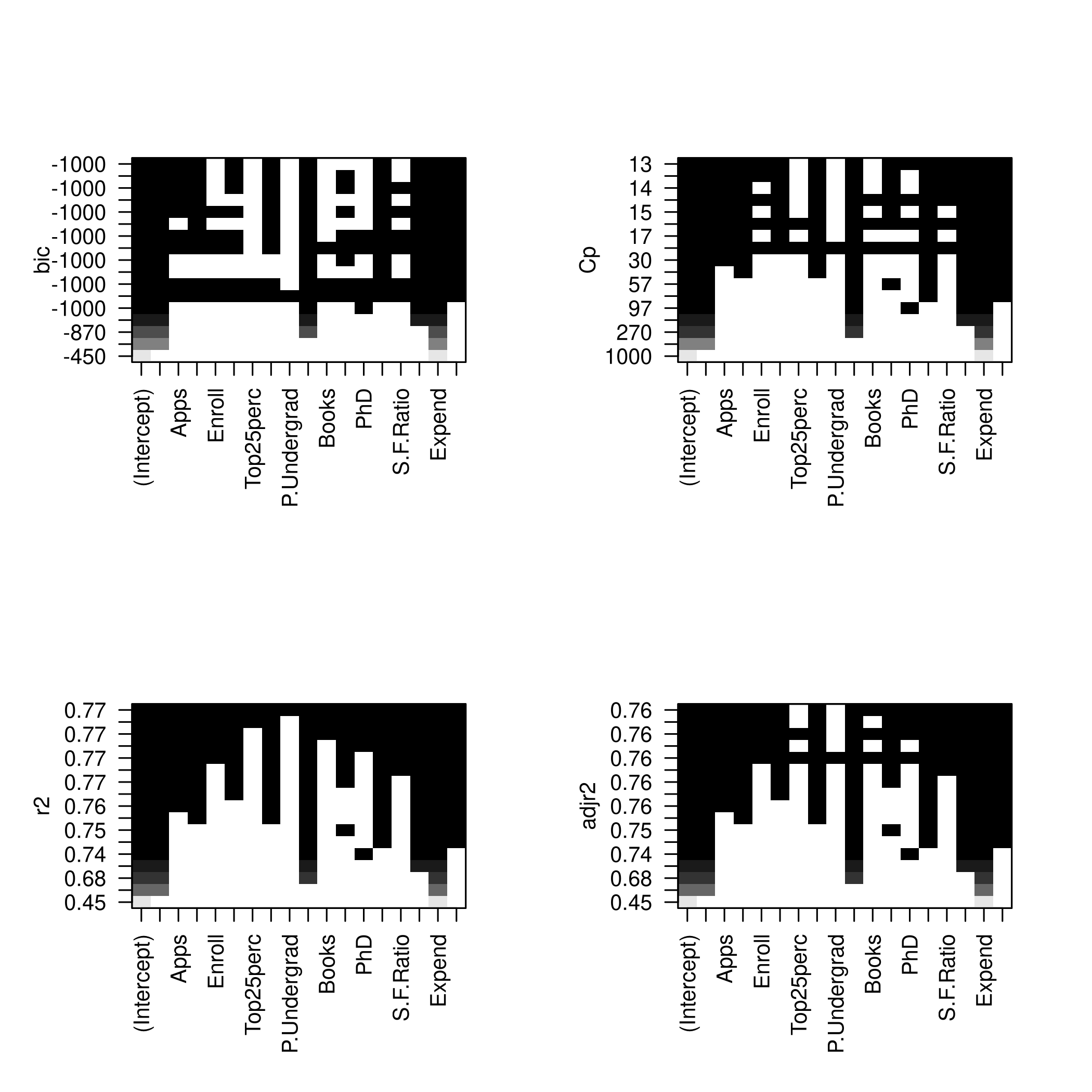
1plotLEAP(modelFit %>% summary)
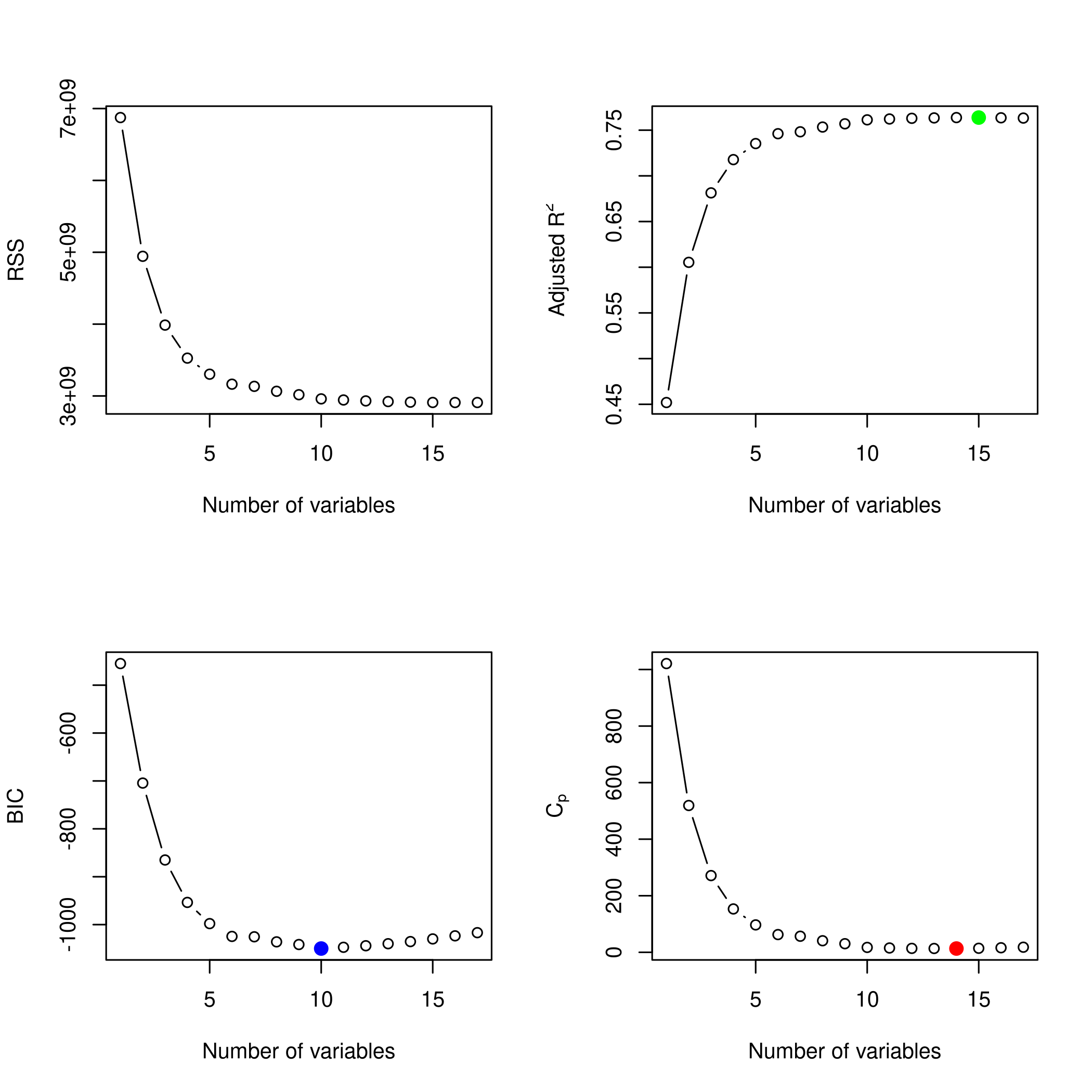
- So we like 14 variables, namely
1coefficients(modelFit,id=14) %>% print
1## (Intercept) PrivateYes Apps Accept Enroll
2## -1.817040e+03 2.256946e+03 -2.999022e-01 8.023519e-01 -5.372545e-01
3## Top10perc F.Undergrad Room.Board Personal PhD
4## 2.365529e+01 -9.569936e-02 8.741819e-01 -2.478418e-01 1.269506e+01
5## Terminal S.F.Ratio perc.alumni Expend Grad.Rate
6## 2.297296e+01 -4.700560e+01 4.195006e+01 2.003912e-01 2.383197e+01
- But five seems like a better bet.
1coefficients(modelFit,id=5)
1## (Intercept) PrivateYes Room.Board PhD perc.alumni
2## -2864.6325619 2936.7416766 1.0677573 40.5334088 61.3147684
3## Expend
4## 0.2253945
b) GAM
1library(gam)
1fit = gam(Outstate ~ Private+s(Apps,3)+Accept+Enroll+
2 Top10perc+F.Undergrad+Room.Board+
3 Personal+PhD+Terminal+S.F.Ratio+
4 perc.alumni+Expend+Grad.Rate
5 , data = colDat)
1## Warning in model.matrix.default(mt, mf, contrasts): non-list contrasts argument
2## ignored
1fit2 = gam(Outstate ~ Private+s(Room.Board,2)+s(PhD,3)+s(perc.alumni)+Expend
2 , data = colDat)
1## Warning in model.matrix.default(mt, mf, contrasts): non-list contrasts argument
2## ignored
1par(mfrow=c(2,2))
2plot(fit,se=TRUE)
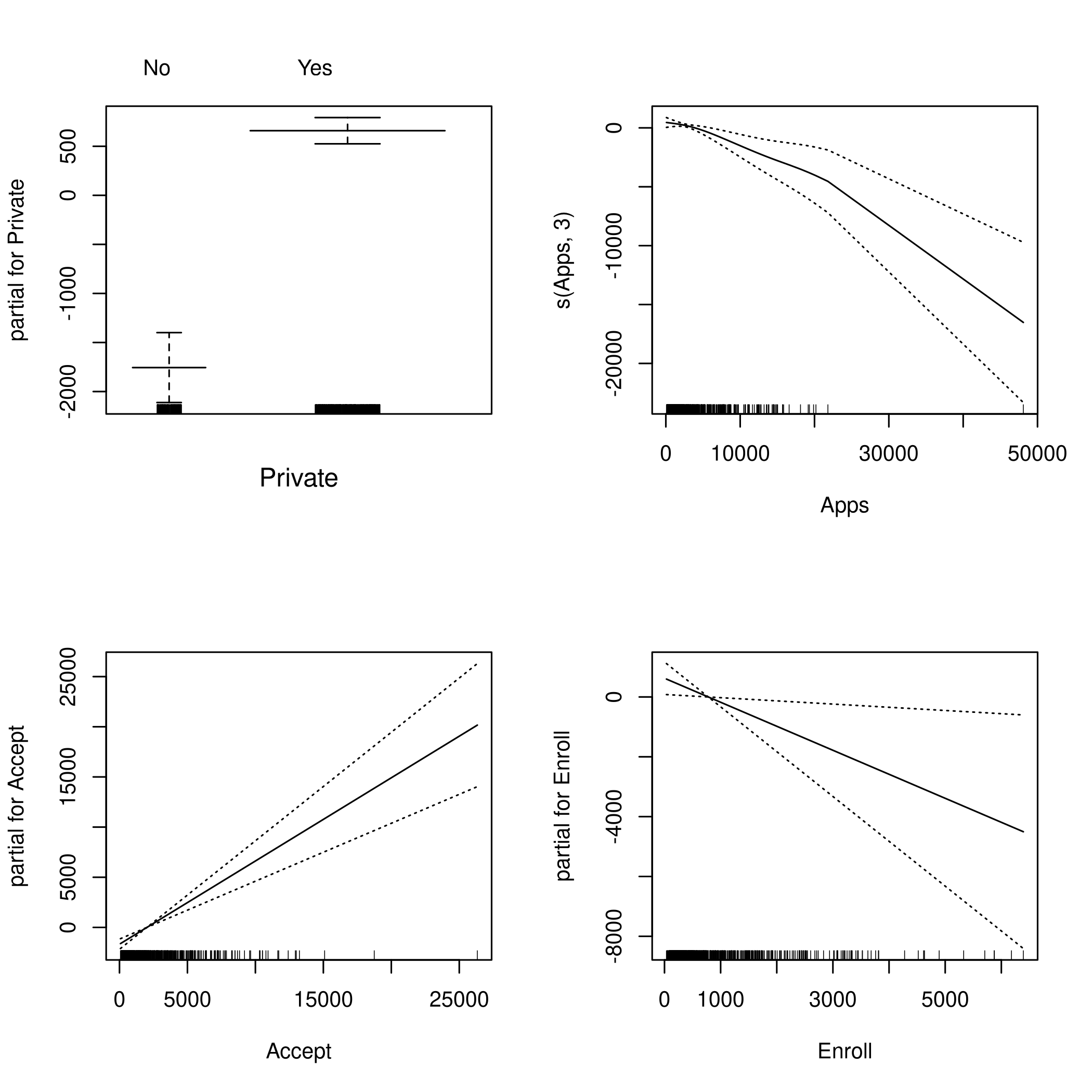
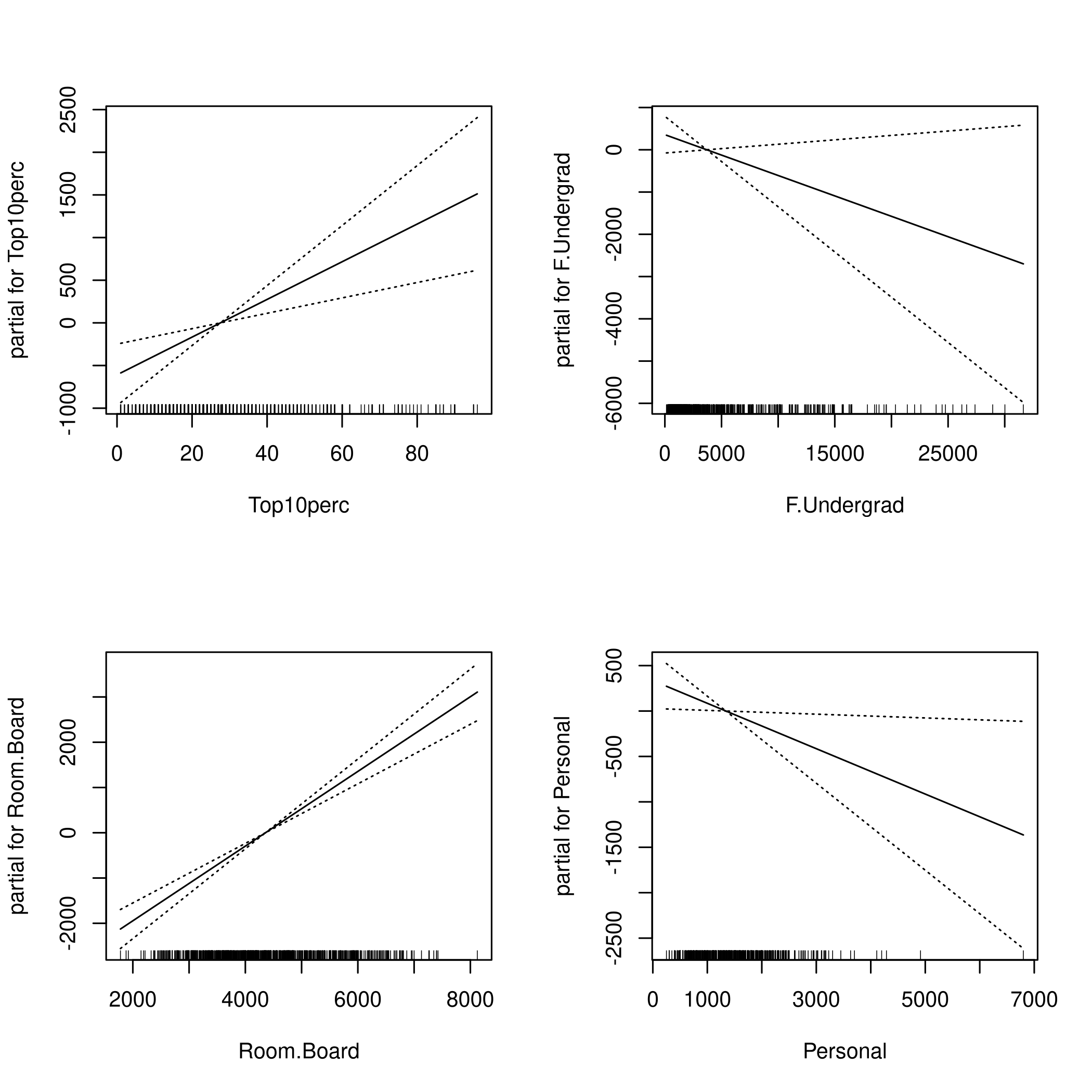
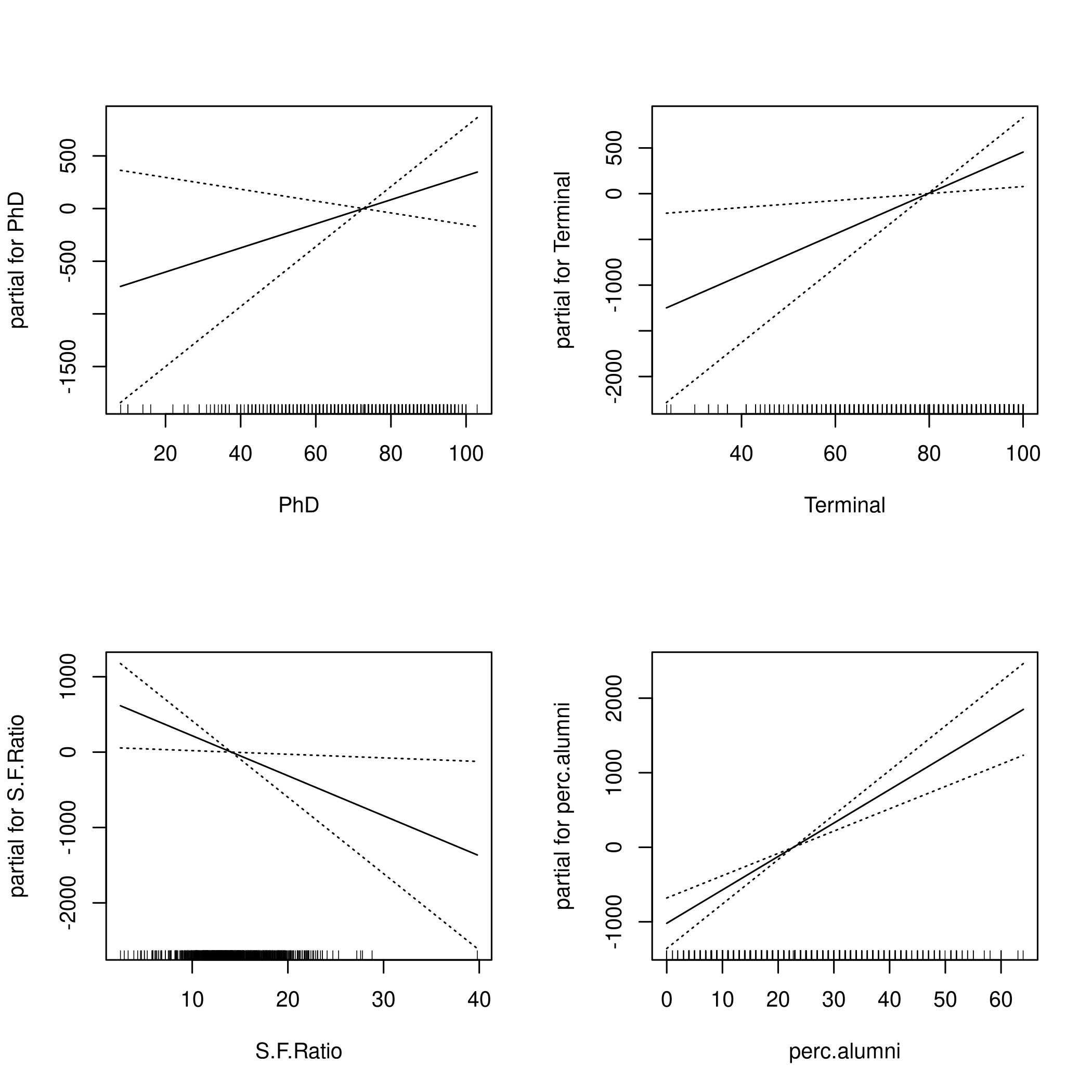
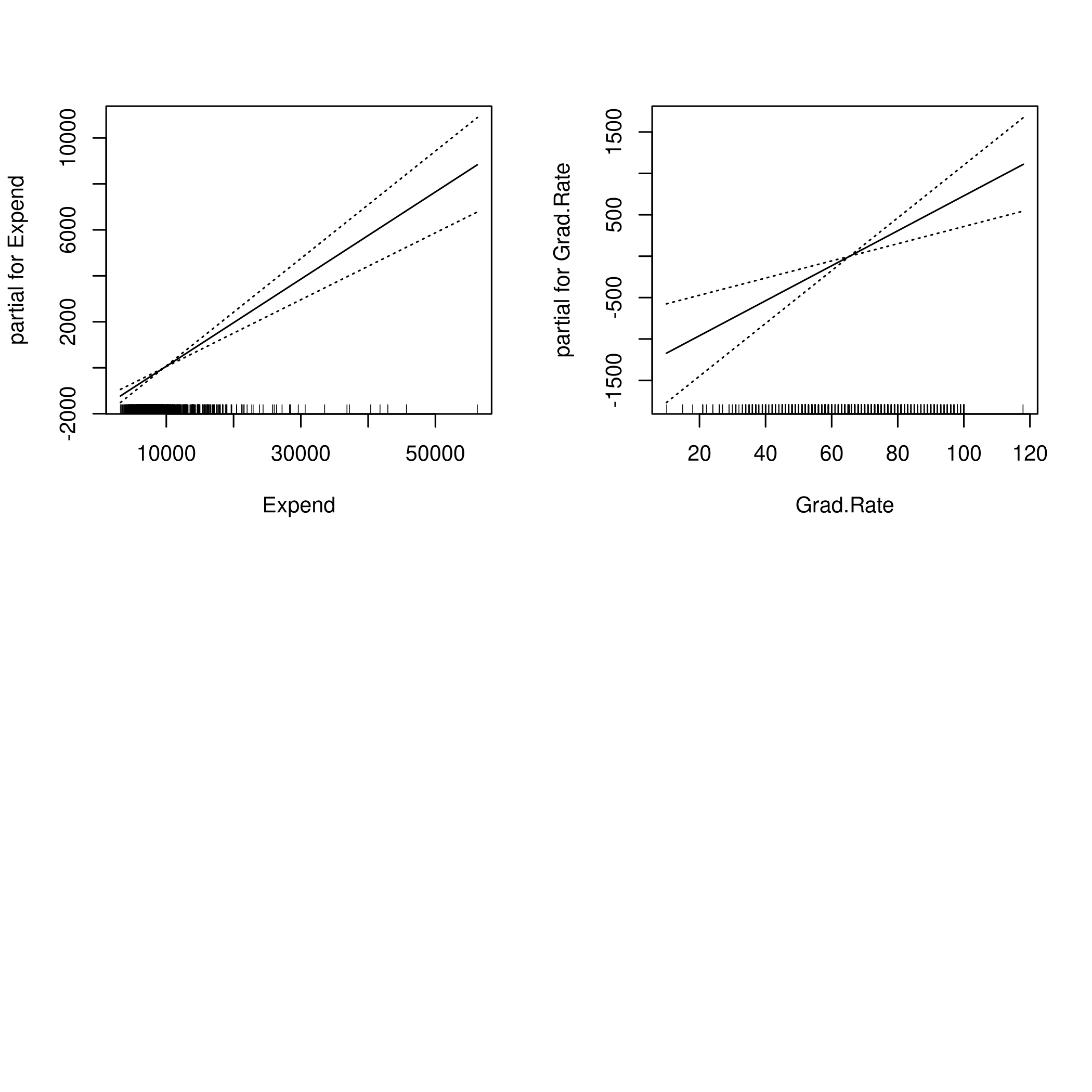
1par(mfrow=c(2,2))
2plot(fit2,se=TRUE)
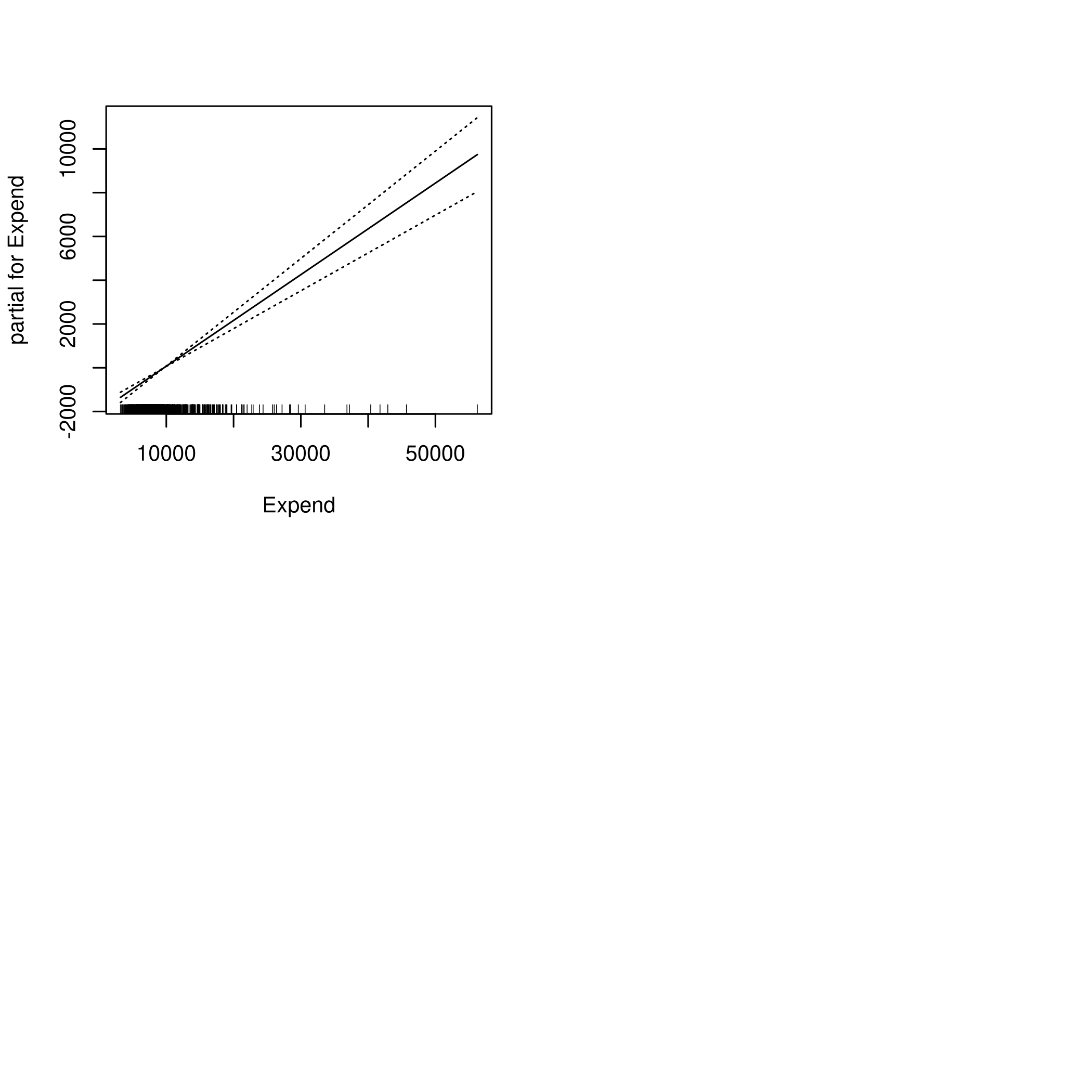
c) Evaluate
1pred <- predict(fit, test_set)
2mse.error <- mean((test_set$Outstate - pred)^2)
3mse.error %>% print
1## [1] 3691891
1gam.tss = mean((test_set$Outstate - mean(test_set$Outstate))^2)
2test.rss = 1 - mse.error/gam.tss
3test.rss %>% print
1## [1] 0.7731239
1pred2 <- predict(fit2, test_set)
2mse.error2 <- mean((test_set$Outstate - pred2)^2)
3mse.error2 %>% print
1## [1] 4121902
1gam.tss2 = mean((test_set$Outstate - mean(test_set$Outstate))^2)
2test.rss2 = 1 - mse.error2/gam.tss2
3test.rss2 %>% print
1## [1] 0.7466987
This is pretty good model, all told.
d) Summary
1summary(fit) %>% print
1##
2## Call: gam(formula = Outstate ~ Private + s(Apps, 3) + Accept + Enroll +
3## Top10perc + F.Undergrad + Room.Board + Personal + PhD + Terminal +
4## S.F.Ratio + perc.alumni + Expend + Grad.Rate, data = colDat)
5## Deviance Residuals:
6## Min 1Q Median 3Q Max
7## -6641.083 -1262.806 -5.698 1270.911 9965.901
8##
9## (Dispersion Parameter for gaussian family taken to be 3749048)
10##
11## Null Deviance: 12559297426 on 776 degrees of freedom
12## Residual Deviance: 2849276343 on 760 degrees of freedom
13## AIC: 13985.3
14##
15## Number of Local Scoring Iterations: 2
16##
17## Anova for Parametric Effects
18## Df Sum Sq Mean Sq F value Pr(>F)
19## Private 1 4034912907 4034912907 1076.250 < 2.2e-16 ***
20## s(Apps, 3) 1 1344548030 1344548030 358.637 < 2.2e-16 ***
21## Accept 1 90544274 90544274 24.151 1.091e-06 ***
22## Enroll 1 144471570 144471570 38.535 8.838e-10 ***
23## Top10perc 1 1802244831 1802244831 480.721 < 2.2e-16 ***
24## F.Undergrad 1 45230645 45230645 12.065 0.0005430 ***
25## Room.Board 1 1110285773 1110285773 296.151 < 2.2e-16 ***
26## Personal 1 47886988 47886988 12.773 0.0003738 ***
27## PhD 1 220249039 220249039 58.748 5.476e-14 ***
28## Terminal 1 66366007 66366007 17.702 2.892e-05 ***
29## S.F.Ratio 1 190811028 190811028 50.896 2.274e-12 ***
30## perc.alumni 1 225293653 225293653 60.094 2.904e-14 ***
31## Expend 1 258162295 258162295 68.861 4.805e-16 ***
32## Grad.Rate 1 57947219 57947219 15.457 9.214e-05 ***
33## Residuals 760 2849276343 3749048
34## ---
35## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
36##
37## Anova for Nonparametric Effects
38## Npar Df Npar F Pr(F)
39## (Intercept)
40## Private
41## s(Apps, 3) 2 8.571 0.0002085 ***
42## Accept
43## Enroll
44## Top10perc
45## F.Undergrad
46## Room.Board
47## Personal
48## PhD
49## Terminal
50## S.F.Ratio
51## perc.alumni
52## Expend
53## Grad.Rate
54## ---
55## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1summary(fit2) %>% print
1##
2## Call: gam(formula = Outstate ~ Private + s(Room.Board, 2) + s(PhD,
3## 3) + s(perc.alumni) + Expend, data = colDat)
4## Deviance Residuals:
5## Min 1Q Median 3Q Max
6## -8676.030 -1345.678 -8.409 1265.524 9590.459
7##
8## (Dispersion Parameter for gaussian family taken to be 4175193)
9##
10## Null Deviance: 12559297426 on 776 degrees of freedom
11## Residual Deviance: 3194023899 on 765.0002 degrees of freedom
12## AIC: 14064.05
13##
14## Number of Local Scoring Iterations: 2
15##
16## Anova for Parametric Effects
17## Df Sum Sq Mean Sq F value Pr(>F)
18## Private 1 3751107814 3751107814 898.43 < 2.2e-16 ***
19## s(Room.Board, 2) 1 2913770756 2913770756 697.88 < 2.2e-16 ***
20## s(PhD, 3) 1 1149711330 1149711330 275.37 < 2.2e-16 ***
21## s(perc.alumni) 1 556759894 556759894 133.35 < 2.2e-16 ***
22## Expend 1 554812125 554812125 132.88 < 2.2e-16 ***
23## Residuals 765 3194023899 4175193
24## ---
25## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
26##
27## Anova for Nonparametric Effects
28## Npar Df Npar F Pr(F)
29## (Intercept)
30## Private
31## s(Room.Board, 2) 1 4.9853 0.0258517 *
32## s(PhD, 3) 2 9.1614 0.0001171 ***
33## s(perc.alumni) 3 0.8726 0.4548496
34## Expend
35## ---
36## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning: with Applications in R. Berlin, Germany: Springer Science & Business Media. ↩︎

